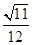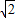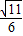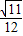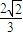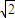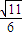题目内容
四面体的五条棱长都是2,另一条棱长为1,则四面体的体积为( )。
A.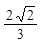 B.
B.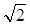 C.
C.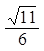 D.
D.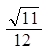
【答案】
C
【解析】
试题分析:设四面体为A-BCD,其中AB=BC=CD=AC=2,AD=1,取AD的中点E,BC的中点F,连接CE、BE、EF,则AD⊥面BCE,BE=CE= ,EF=
,EF= ,所以
,所以 .
.
考点:三棱锥的体积公式。
点评:要求四面体的体积关键是求出四面体的高,做此题的关键是把四面体A-BCD的体积转化为三棱锥-BCE和三棱锥C-BCE的体积之和。此题为中档题。

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
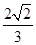 B.
B.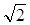 C.
C.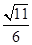 D.
D.