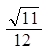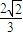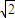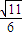题目内容
四面体的五条棱长都是2,另一条棱长为1,则四面体的体积为( )A.

B.
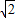
C.
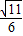
D.
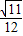
【答案】分析:由题意如图,三棱锥的三条侧棱长为:2,底面边长分别为:2,2,1,取AC的中点O,利用平面PBO将四面体分割成两部分,这两部分都是以面PBO为底,高分别为AO,CO的三棱锥,最后利用三棱锥的体积公式求解即可.
解答: 解:由题意画出图形,PA=PB=PC=BC=AB=2,AC=1,
解:由题意画出图形,PA=PB=PC=BC=AB=2,AC=1,
所以△ABC是等腰三角形,O为AC的中点,AC垂直截面PBO;
易知PO=BO= =
= ,
,
在等腰三角形PBO中,底边PB上的高为 =
= ;
;
则四面体的体积为:V= =
= ×
× ×2×
×2× ×1=
×1= ,
,
故选C.
点评:本题是基础题,考查棱锥的体积的求法,正确处理棱锥的棱长之间的数据关系,AC垂直截面PBO,是本题解决的关键,考查空间想象能力,计算能力.
解答:
 解:由题意画出图形,PA=PB=PC=BC=AB=2,AC=1,
解:由题意画出图形,PA=PB=PC=BC=AB=2,AC=1,所以△ABC是等腰三角形,O为AC的中点,AC垂直截面PBO;
易知PO=BO=
 =
= ,
,在等腰三角形PBO中,底边PB上的高为
 =
= ;
;则四面体的体积为:V=
 =
= ×
× ×2×
×2× ×1=
×1= ,
,故选C.
点评:本题是基础题,考查棱锥的体积的求法,正确处理棱锥的棱长之间的数据关系,AC垂直截面PBO,是本题解决的关键,考查空间想象能力,计算能力.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
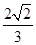 B.
B.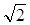 C.
C.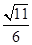 D.
D.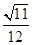
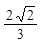 B.
B.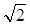 C.
C.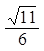 D.
D.