题目内容

精英家教网如图，设B、C两点在河的两岸，一测量者在B所在的同侧河岸边选定一点A，测出AB的距离为100m，∠ABC=105°，∠CAB=45°后，就可以计算出B、C两点的距离为（　　）
A、50
3
m
B、50
2
m
C、100
3
m
D、100
2
m
分析：依题意在A，B，C三点构成的三角形中利用正弦定理，根据AB，∠ACB，∠CAB的值，即可求得BC．
解答：解：由三角形内角和公式可得∠ACB=30°，再由正弦定理可得
AB
sin∠ACB
=
BC
sin∠CAB
，
即
100
1
2
=
BC
2
2
，解得BC=100
2
m．
故选：D．
点评：本题主要考查正弦定理的应用，三角形的内角和公式，属于中档题．
练习册系列答案
相关题目
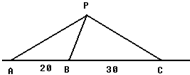精英家教网如图所示，在一条海防警戒线上的点A、B、C处各有一个水声监测点，B、C两点到点A的距离分别为20千米和50千米．某时刻，B收到发自静止目标P的一个声波信号，8秒后A、C同时接收到该声波信号，已知声波在水中的传播速度是1.5千米/秒．
（1）设A到P的距离为x千米，用x表示B，C到P的距离，并求x的值；
（2）求P到海防警戒线AC的距离（结果精确到0.01千米）．
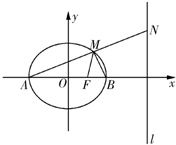精英家教网如图，已知椭圆C：
x2
16
+
y2
12
=1的左、右顶点分别为A、B，右焦点为F，直线l为椭圆的右准线，N为l上一动点，且在x轴上方，直线AN与椭圆交于点M．
（1）若AM=MN，求∠AMB的余弦值；
（2）设过A，F，N三点的圆与y轴交于P，Q两点，当线段PQ的中点坐标为（0，9）时，求这个圆的方程．
（2013•潍坊一模）如图，已知圆C与y轴相切于点T（0，2），与x轴正半轴相交于两点M，N（点M必在点N的右侧），且|MN|=3椭圆D：
x2
a2
+
y2
b2
=1(a＞b＞0)的焦距等于2|ON|，且过点(
2
，
6
2
)．
（I） 求圆C和椭圆D的方程；
（Ⅱ） 设椭圆D与x轴负半轴的交点为P，若过点M的动直线l与椭圆D交于A、B两点，∠ANM=∠BNP是否恒成立？给出你的判断并说明理由．
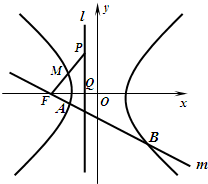如图点F为双曲线C的左焦点，左准线l交x轴于点Q，点P是l上的一点|PQ|=|FQ|=1，且线段PF的中点M在双曲线C的左支上．
（1）求双曲线C的标准方程；
（2）若过点F的直线m与双曲线C的左右两支分别交于A、B两点，设
FB
=λ
FA
，当λ∈[6，+∞）时，求直线m的斜率k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网