题目内容
函数f(x)=lg 是奇函数,则实常数a的值为________.
是奇函数,则实常数a的值为________.
-1
分析:先根据奇函数的定义得到a的值,再结合定义域关于原点对称即可确定实常数a的值.
解答:因为函数f(x)=lg 是奇函数;
是奇函数;
所以:f(-x)+f(x)=0?lg +lg
+lg =0?lg
=0?lg =0?
=0? =1.
=1.
∴a=±1,
当a=1时,f(x)=lg =1,定义域为{x|x≠-2}不关于原点对称,舍;
=1,定义域为{x|x≠-2}不关于原点对称,舍;
当a=-1时,f(x)=lg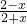 成立.
成立.
故答案为:-1.
点评:本题主要考查函数奇偶性的性质.一个函数存在奇偶性的前提是定义域关于原点对称.
分析:先根据奇函数的定义得到a的值,再结合定义域关于原点对称即可确定实常数a的值.
解答:因为函数f(x)=lg
 是奇函数;
是奇函数;所以:f(-x)+f(x)=0?lg
 +lg
+lg =0?lg
=0?lg =0?
=0? =1.
=1.∴a=±1,
当a=1时,f(x)=lg
 =1,定义域为{x|x≠-2}不关于原点对称,舍;
=1,定义域为{x|x≠-2}不关于原点对称,舍;当a=-1时,f(x)=lg
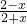 成立.
成立.故答案为:-1.
点评:本题主要考查函数奇偶性的性质.一个函数存在奇偶性的前提是定义域关于原点对称.

练习册系列答案
相关题目
 是( )
是( )