题目内容
对于函数f(x),如果存在锐角θ使得f(x)的图象绕坐标原点逆时针旋转角θ,所得曲线仍是一函数,则称函数f(x)具备角θ的旋转性,下列函数具有角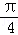 的旋转性的是( )
的旋转性的是( )
A.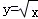 | B.y=lnx | C.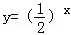 | D.y=x2 |
C
解析试题分析:若若函数f(x)逆时针旋转角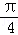 后所得曲线仍是一函数,根据函数的定义中的“唯一性”可得函数f(x)的图象与任一斜率为1的直线y=x+b均不能有两个以上的交点,逐一分析四个答案中的函数是否满足这一性质,可得答案.
后所得曲线仍是一函数,根据函数的定义中的“唯一性”可得函数f(x)的图象与任一斜率为1的直线y=x+b均不能有两个以上的交点,逐一分析四个答案中的函数是否满足这一性质,可得答案.
解:若函数f(x)逆时针旋转角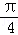 后所得曲线仍是一函数,
后所得曲线仍是一函数,
则函数f(x)的图象与任一斜率为1的直线y=x+b均不能有两个以上的交点
A中函数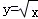 与直线y=x有两个交点,不满足要求;
与直线y=x有两个交点,不满足要求;
B中函数y=lnx与直线y=x﹣1有两个交点,不满足要求;
C中函数 与直线y=x+b均有且只有一个交点,满足要求;
与直线y=x+b均有且只有一个交点,满足要求;
D中函数y=x2与直线y=x有两个交点,不满足要求;
故选C
点评:本题考查的知识点是函数的定义,其中根据函数的定义分析出函数f(x)的图象与任一斜率为1的直线y=x+b均不能有两个以上的交点,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知数列{a }的前n项和
}的前n项和 满足:
满足: ,且
,且 =1.那么
=1.那么 =( )
=( )
| A.1 | B.9 | C.10 | D.55 |
若直线 通过点
通过点 ,则( )
,则( )
A. | B. | C. | D. |
阅读下图中的算法,其功能是( ).
第一步,m = a.
第二步,b<m,则m = b.
第三步,若c<m,则m = c.
第四步,输出m.
| A.将a,b,c由小到大排序 | B.将a,b,c由大到小排序 |
| C.输出a,b,c中的最大值 | D.输出a,b,c中的最小值 |
 的通项公式是_______.
的通项公式是_______.
 <6的解集为(﹣1,1),则实数a等于 .
<6的解集为(﹣1,1),则实数a等于 .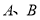 为两个定点,
为两个定点,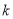 为非零常数,
为非零常数, ,则动点
,则动点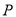 的轨迹为双曲线;
的轨迹为双曲线; 上一定点
上一定点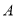 作圆的动点弦
作圆的动点弦 ,
,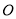 为坐标原点,若
为坐标原点,若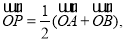 则动点
则动点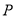 的轨迹为圆;
的轨迹为圆; ,则双曲线
,则双曲线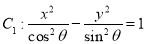 与
与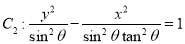 的离心率相同;
的离心率相同; 和一动点
和一动点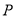 ,若
,若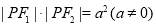 ,则点
,则点 的轨迹关于原点对称.
的轨迹关于原点对称. 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
 表示出储油灌的容积
表示出储油灌的容积 ,并写出
,并写出 的范围.
的范围. 与半径
与半径 的比为多少时,储油灌的容积
的比为多少时,储油灌的容积 在定义域
在定义域 上单调递减,求满足
上单调递减,求满足 的实数
的实数 的取值范围.
的取值范围.