题目内容
(本题满分16分)如图,储油灌的表面积 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.

(1)试用半径 表示出储油灌的容积
表示出储油灌的容积 ,并写出
,并写出 的范围.
的范围.
(2)当圆柱高 与半径
与半径 的比为多少时,储油灌的容积
的比为多少时,储油灌的容积 最大?
最大?
(1)

(2)圆柱高 与半径
与半径 的比为1时,储油灌的容积
的比为1时,储油灌的容积 最大.
最大.
【解析】
试题分析:(1)由储油灌的表面积可求得下部圆柱的高.储油灌的容积等于半球的体积与圆柱体积的和.根据下部圆柱的高为正数可求得 的范围.(2)先将(1)中所得
的范围.(2)先将(1)中所得 求导,令导数等于0.讨论导数的正负,可得函数的单调性,根据其单调性可求其最值.
求导,令导数等于0.讨论导数的正负,可得函数的单调性,根据其单调性可求其最值.
试题解析:(1) ,
, , 3分
, 3分

 ; 7分
; 7分
(2) ,令
,令 ,得
,得 , 9分
, 9分
列表

13分
∴当 时,体积
时,体积 取得最大值,此时
取得最大值,此时 ,
, 16分
16分
考点:导数的应用问题.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
直线 平行,则
平行,则 等于( )
等于( )
A. | B. | C.0 | D. |
计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制数的对应关系如下表:
十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如,用十六进制表示:E+D=1B,则B×F (“×”表示通常的乘法运算)等于( )
A.A5 B.BF C.165 D.B9
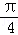 的旋转性的是( )
的旋转性的是( )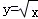
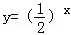
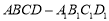 的棱长为
的棱长为 ,点
,点 在棱
在棱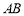 上,且
上,且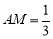 ,点
,点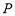 是平面
是平面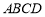 上的动点,且动点
上的动点,且动点 的距离与点
的距离与点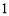 ,则动点
,则动点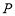 的轨迹是 ( )
的轨迹是 ( ) 
 是椭圆
是椭圆 上的动点,
上的动点, 为椭圆的左焦点,定点
为椭圆的左焦点,定点 ,则
,则 的最大值为 _______
的最大值为 _______  中,
中, 则
则 边上的高
边上的高 的长为 ;
的长为 ; 的图象, 可能正确的是( )
的图象, 可能正确的是( )