题目内容
若 上是减函数,则
上是减函数,则 的取值范围是( )
的取值范围是( )
A. | B. | C.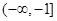 | D. |
C
解析试题分析:根据题意,由于
是减函数,则说明其导数 恒成立,可知分母大于零,则分子恒小于等于零,得到
恒成立,可知分母大于零,则分子恒小于等于零,得到 ,结合二次函数的性质可知,只要b小于二次函数的最小值即可,由于开口向上,对称轴为x=1,定义域为x<-1,则可知函数的最小值为-1,故可知答案为
,结合二次函数的性质可知,只要b小于二次函数的最小值即可,由于开口向上,对称轴为x=1,定义域为x<-1,则可知函数的最小值为-1,故可知答案为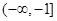 ,选C.
,选C.
考点:函数的单调性
点评:主要是考查了函数单调性的判定以及参数范围的求解,属于基础题。

练习册系列答案
相关题目
若在曲线 上两个不同点处的切线重合,则称这条切线为曲线
上两个不同点处的切线重合,则称这条切线为曲线 或
或 的“自公切线”。
的“自公切线”。
下列方程:
① ;
;
② ;
;
③ ;
;
④
对应的曲线中存在“自公切线”的有( )
| A.①③ | B.①④ | C.②③ | D.②④ |
设定义在 上的函数
上的函数 , 若关于
, 若关于 的方程
的方程 有3个不同实数解
有3个不同实数解 ,且
,且 ,则下列说法中错误的是:( )
,则下列说法中错误的是:( )
A. | B. | C. | D. |
已知函数
A. | B. | C. | D. |
正弦曲线 通过坐标变换公式
通过坐标变换公式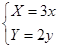 ,变换得到的新曲线为
,变换得到的新曲线为
A.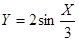 | B.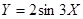 | C.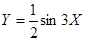 | D.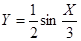 |
定义在 上的奇函数
上的奇函数 满足
满足 ,当
,当 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知函数 对定义域
对定义域 内的任意
内的任意 都有
都有 =
= ,且当
,且当 时其导函数
时其导函数 满足
满足 若
若 则 ( )
则 ( )
A. | B. |
C. | D. |
定义域为 的四个函数
的四个函数 ,
, ,
, ,
, 中,奇函数的个数是( )
中,奇函数的个数是( )
A. | B. | C. | D. |
 的部分图象是( )
的部分图象是( )