题目内容
【题目】已知函数![]() (
(![]() ).
).
(1)若函数![]() 有两个零点,求实数a的取值范围
有两个零点,求实数a的取值范围
(2)证明:![]()
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)令![]() ,得到
,得到![]() ,令
,令![]() ,
,![]() ,利用导数求得函数
,利用导数求得函数![]() 的单调性与最小值
的单调性与最小值![]() ,要使函数
,要使函数![]() 有两个零点,则函数
有两个零点,则函数![]() 的图象与
的图象与![]() 有两个不同的交点,即可求解;
有两个不同的交点,即可求解;
(2)要证明![]() ,只需
,只需![]() ,令
,令![]() ,利用导数求得函数的
,利用导数求得函数的![]() 的单调性与最值,即可求解.
的单调性与最值,即可求解.
(1)由题意,函数![]() 的定义域为
的定义域为![]() ,
,
令![]() ,则
,则![]() ,
,
记![]() ,
,![]() ,
,
则![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以![]() 有最小值,且为
有最小值,且为![]() ,
,
又当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以要使函数![]() 有两个零点,则函数
有两个零点,则函数![]() 的图象与
的图象与![]() 有两个不同的交点,
有两个不同的交点,
则![]() ,即实数a的取值范围为
,即实数a的取值范围为![]() .
.
(2)由(1)知,函数![]() 有最小值为
有最小值为![]() ,可得
,可得![]() ,
,
当且仅当![]() 时取等号,
时取等号,
因此要证明![]() ,
,
即只需要证明![]() ,
,
记![]() ,则
,则![]()
![]() ,
,
令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以![]() ,
,
即![]() 恒成立,当且仅当
恒成立,当且仅当![]() 时取等号,
时取等号,
所以![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.

练习册系列答案
相关题目
【题目】某种植物感染![]() 病毒极易导致死亡,某生物研究所为此推出了一种抗
病毒极易导致死亡,某生物研究所为此推出了一种抗![]() 病毒的制剂,现对
病毒的制剂,现对![]() 株感染了
株感染了![]() 病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计;并对植株吸收制剂的量(单位:
病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计;并对植株吸收制剂的量(单位:![]() )进行统计规定:植株吸收在
)进行统计规定:植株吸收在![]() (包括
(包括![]() )以上为“足量”,否则为“不足量”.现对该
)以上为“足量”,否则为“不足量”.现对该![]() 株植株样本进行统计,其中“植株存活”的
株植株样本进行统计,其中“植株存活”的![]() 株,对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共
株,对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共![]() 株.
株.
编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
吸收量 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)完成以![]() 下列联表,并判断是否可以在犯错误概率不超过
下列联表,并判断是否可以在犯错误概率不超过![]() 的前提下,认为“植株的存活”与“制剂吸收足量”有关?
的前提下,认为“植株的存活”与“制剂吸收足量”有关?
吸收足量 | 吸收不足量 | 合计 | |
植株存活 |
| ||
植株死亡 | |||
合计 |
|
(2)若在该样本“制剂吸收不足量”的植株中随机抽取![]() 株,求这
株,求这![]() 株中恰有
株中恰有![]() 株“植株存活”的概率.
株“植株存活”的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
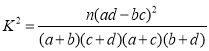 ,其中
,其中![]()