题目内容
设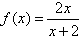
，x1=1，xn=f（xn-1）（n≥2，n∈N*），
（Ⅰ）求x2，x3，x4的值；
（Ⅱ）归纳{xn}的通项公式，并用数学归纳法证明.
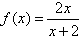，x1=1，xn=f（xn-1）（n≥2，n∈N*），（Ⅰ）求x2，x3，x4的值；
（Ⅱ）归纳{xn}的通项公式，并用数学归纳法证明.
解：（Ⅰ）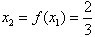
，
，
；
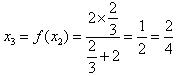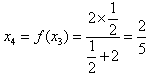（Ⅱ）根据计算结果，可以归纳出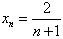
；
当n=1时，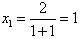
，与已知相符，归纳出的公式成立；
假设当n=k（k∈N*）时，公式成立，即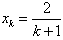
，
那么，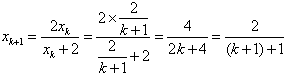
，
所以，当n=k+1时，公式也成立；
综上，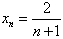
对于任何n∈N*都成立。
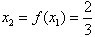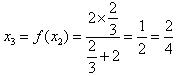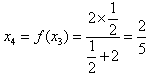，，；（Ⅱ）根据计算结果，可以归纳出
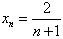；当n=1时，
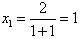，与已知相符，归纳出的公式成立；假设当n=k（k∈N*）时，公式成立，即
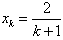，那么，
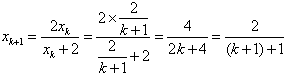，所以，当n=k+1时，公式也成立；
综上，
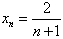对于任何n∈N*都成立。
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
，x1=1，xn=f（xn-1）（n≥2，n∈N*）．