题目内容
以下命题正确的个数为（ ）
①若a2+b2=8，则ab的最大值为4；
②若a＞0，b＞0，且a+b=4，则
+
的最小值为1；
③若x∈R，则x+
的最小值为6；
④若x＞0，y＞0，且4x+y=1，则xy的最大值为
．
①若a2+b2=8，则ab的最大值为4；
②若a＞0，b＞0，且a+b=4，则
| 1 |
| a |
| 1 |
| b |
③若x∈R，则x+
| 4 |
| x-2 |
④若x＞0，y＞0，且4x+y=1，则xy的最大值为
| 1 |
| 4 |
| A．1 | B．2 | C．3 | D．4 |
由①知，a2+b2=8，
∴ab≤
=4成立（当且仅当a=b=2或a=b=-2时，取等号），故①正确．
由②知，a+b=4，∴
+
=1．
∴
+
=(
+
)(
+
)=
+
+
+
≥
+2
=
+
=1（当且仅当a=b=2时取等号），故③正确．
由③x∈R，不能保证x-2为正数，此函数没有最小值，判断③不正确；
④：xy=
4x•y≤
(
)2=
，当且仅当4x=y=
时取等号．
则xy的最大值为：
．故④不正确．
故正确的有①②．
故选B．
∴ab≤
| a2+b2 |
| 2 |
由②知，a+b=4，∴
| a |
| 4 |
| b |
| 4 |
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| a |
| 4 |
| b |
| 4 |
| 1 |
| 4 |
| b |
| 4a |
| a |
| 4b |
| 1 |
| 4 |
≥
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
由③x∈R，不能保证x-2为正数，此函数没有最小值，判断③不正确；
④：xy=
| 1 |
| 4 |
| 1 |
| 4 |
| 4x+y |
| 2 |
| 1 |
| 16 |
| 1 |
| 2 |
则xy的最大值为：
| 1 |
| 16 |
故正确的有①②．
故选B．
练习册系列答案
相关题目
的最小值为1；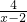
的最小值为6；
．
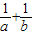的最小值为1；
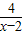的最小值为6；
．