题目内容
以下命题正确的个数为
①若a2+b2=8,则ab的最大值为4;
②若a>0,b>0,且a+b=4,则 的最小值为1;
的最小值为1;
③若x∈R,则x+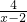 的最小值为6;
的最小值为6;
④若x>0,y>0,且4x+y=1,则xy的最大值为 .
.
- A.1
- B.2
- C.3
- D.4
B
分析:根据ab≤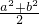 推断①正确;
推断①正确;
利用 +
+ =
= 展开后根据均值不等式求得
展开后根据均值不等式求得  +
+ 的最小值判断出②正确;
的最小值判断出②正确;
根据x∈R,不能保证x-2为正数,判断③不正确;
对于④变形为4x与y的乘积,利用 基本不等式求最大值,推断④不正确.
解答:由①知,a2+b2=8,
∴ab≤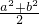 =4成立(当且仅当a=b=2或a=b=-2时,取等号),故①正确.
=4成立(当且仅当a=b=2或a=b=-2时,取等号),故①正确.
由②知,a+b=4,∴ +
+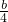 =1.
=1.
∴ +
+ =
= =
= +
+ +
+ +
+
≥ +2
+2  =
= +
+ =1(当且仅当a=b=2时取等号),故③正确.
=1(当且仅当a=b=2时取等号),故③正确.
由③x∈R,不能保证x-2为正数,此函数没有最小值,判断③不正确;
④: ,当且仅当4x=y=
,当且仅当4x=y= 时取等号.
时取等号.
则xy的最大值为: .故④不正确.
.故④不正确.
故正确的有①②.
故选B.
点评:本题主要考查了基本不等式在求最值问题的应用.要特别留意基本不等式中等号成立的条件.
分析:根据ab≤
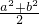 推断①正确;
推断①正确;利用
 +
+ =
= 展开后根据均值不等式求得
展开后根据均值不等式求得  +
+ 的最小值判断出②正确;
的最小值判断出②正确;根据x∈R,不能保证x-2为正数,判断③不正确;
对于④变形为4x与y的乘积,利用 基本不等式求最大值,推断④不正确.
解答:由①知,a2+b2=8,
∴ab≤
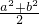 =4成立(当且仅当a=b=2或a=b=-2时,取等号),故①正确.
=4成立(当且仅当a=b=2或a=b=-2时,取等号),故①正确.由②知,a+b=4,∴
 +
+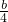 =1.
=1.∴
 +
+ =
= =
= +
+ +
+ +
+
≥
 +2
+2  =
= +
+ =1(当且仅当a=b=2时取等号),故③正确.
=1(当且仅当a=b=2时取等号),故③正确.由③x∈R,不能保证x-2为正数,此函数没有最小值,判断③不正确;
④:
 ,当且仅当4x=y=
,当且仅当4x=y= 时取等号.
时取等号.则xy的最大值为:
 .故④不正确.
.故④不正确.故正确的有①②.
故选B.
点评:本题主要考查了基本不等式在求最值问题的应用.要特别留意基本不等式中等号成立的条件.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
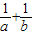 的最小值为1;
的最小值为1;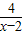 的最小值为6;
的最小值为6; .
.