题目内容
设 .
.(1)当
 时,求f(x)的值域;
时,求f(x)的值域;(2)把f(x)的图象向右平移m(m>0)个单位后所得图象关于y轴对称,求m的最小值.
【答案】分析:(1)利用三角函数的恒等变换化简f(x)的解析式为2cos(4x+ ),通过x的范围求出相位的范围,由此求得f(x)的值域.
),通过x的范围求出相位的范围,由此求得f(x)的值域.
(2)先求出平移后函数due解析式,根据图象关于直线x=0对称,故有-4m+ =kπ,k∈Z,由此求得正数m的最小值.
=kπ,k∈Z,由此求得正数m的最小值.
解答:解:(1)∵f(x)=4cos2x•( cos2x-
cos2x- sin2x)-1=2cos22x-2
sin2x)-1=2cos22x-2 sin2x•cos2x-1
sin2x•cos2x-1
=cos4x- sin4x=2cos(4x+
sin4x=2cos(4x+ ),(4分)
),(4分)
因为
∴4x+ ∈
∈ ,
,
f(x)的最小值为-2,函数的最大值为:1.(6分)
∴f(x)的值域:[-2,1].(7分)
(2)f(x)图象向右平移m个单位后所得图象对应的解析式为
y=2cos[4(x-m)+ ]=2cos(4x-4m+
]=2cos(4x-4m+ ),(9分)
),(9分)
其为偶函数,那么图象关于直线x=0对称,故有:-4m+ =kπ,k∈Z
=kπ,k∈Z
∴m= 所以正数m的最小值为
所以正数m的最小值为 .(12分).
.(12分).
点评:本题主要考查三角函数的恒等变换及化简求值,函数y=Asin(ωx+∅)的图象变换,属于中档题.
 ),通过x的范围求出相位的范围,由此求得f(x)的值域.
),通过x的范围求出相位的范围,由此求得f(x)的值域.(2)先求出平移后函数due解析式,根据图象关于直线x=0对称,故有-4m+
 =kπ,k∈Z,由此求得正数m的最小值.
=kπ,k∈Z,由此求得正数m的最小值.解答:解:(1)∵f(x)=4cos2x•(
 cos2x-
cos2x- sin2x)-1=2cos22x-2
sin2x)-1=2cos22x-2 sin2x•cos2x-1
sin2x•cos2x-1=cos4x-
 sin4x=2cos(4x+
sin4x=2cos(4x+ ),(4分)
),(4分)因为

∴4x+
 ∈
∈ ,
,f(x)的最小值为-2,函数的最大值为:1.(6分)
∴f(x)的值域:[-2,1].(7分)
(2)f(x)图象向右平移m个单位后所得图象对应的解析式为
y=2cos[4(x-m)+
 ]=2cos(4x-4m+
]=2cos(4x-4m+ ),(9分)
),(9分)其为偶函数,那么图象关于直线x=0对称,故有:-4m+
 =kπ,k∈Z
=kπ,k∈Z∴m=
 所以正数m的最小值为
所以正数m的最小值为 .(12分).
.(12分).点评:本题主要考查三角函数的恒等变换及化简求值,函数y=Asin(ωx+∅)的图象变换,属于中档题.

练习册系列答案
相关题目
 .
. 时,求f(x)的值域;
时,求f(x)的值域;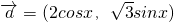 ,
,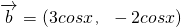 ,设
,设 ,
,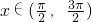 时,求f(x)的最小值及取得最小值时x的取值集合;
时,求f(x)的最小值及取得最小值时x的取值集合;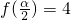 ,求
,求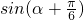 的值.
的值.
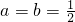 时,求f(x)的最大值.
时,求f(x)的最大值.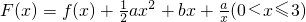 ,以其图象上任一点P(x0,y0)为切点的切线的斜率
,以其图象上任一点P(x0,y0)为切点的切线的斜率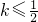 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
 时,求f(x)的最大值.
时,求f(x)的最大值. ,以其图象上任一点P(x,y)为切点的切线的斜率
,以其图象上任一点P(x,y)为切点的切线的斜率 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.