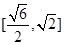题目内容
直线 与圆
与圆 相交于
相交于 ,
, 两点,且
两点,且 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
A
解析试题分析:如图,圆 的圆心C(3,2),半径
的圆心C(3,2),半径 ,求得圆心C(3,2)到直线
,求得圆心C(3,2)到直线 的距离
的距离 ,由勾股定理得:
,由勾股定理得: ,因为
,因为 ,所以
,所以 ,则
,则 ,解得
,解得 。故选A。
。故选A。
考点:直线与圆的位置关系
点评:关于直线与圆的位置关系的题目,一般情况下,结合圆心到直线的距离对解决问题有很大的作用。

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
两圆 和
和 的位置关系是( )
的位置关系是( )
| A.相交 | B.外切 | C.内切 | D.外离 |
若直线 与圆
与圆 相切,则
相切,则 的值为( )
的值为( )
A. | B. | C. | D. 或 或 |
 表示一个圆,则
表示一个圆,则 的取值范围是( )
的取值范围是( )
A. ≤2 ≤2 | B. | C. | D. ≤ ≤ |
若直线 平分圆
平分圆 ,则
,则 的最小值是
的最小值是
A. | B. | C. | D. |
两圆相交于点A(1,3)、B(m,-1),两圆的圆心均在直线x-y+c=0上,则m+c的值为( )
| A.3 | B.2 | C.0 | D.-1 |
直线 截圆
截圆 所得劣弧所对的圆心角是
所得劣弧所对的圆心角是
A.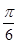 | B. |
C. | D. |
 上一动点,PA,PB是圆C:
上一动点,PA,PB是圆C: 的两条切线,A、B是切点,若四边形PACB的最小面积是2,则
的两条切线,A、B是切点,若四边形PACB的最小面积是2,则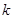 的值为
的值为  C.
C. D.2
D.2 (a>0,b>0)的左右焦点分别为F1,F2,P为双曲线上任一点,已知|
(a>0,b>0)的左右焦点分别为F1,F2,P为双曲线上任一点,已知| |·|
|·| |的最小值为m.当
|的最小值为m.当 ≤m≤
≤m≤ 时,其中c=
时,其中c= ,则双曲线的离心率e的取值范围是 ( )
,则双曲线的离心率e的取值范围是 ( )