题目内容
定义min{a,b}=
,若f(x)=min{
,a-x2}的最大值为3,则a等于
|
| x+5 |
| 2 |
4
4
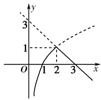
.分析:令y1=
,y2=a-x2,在同一坐标系内作出y1和y2的图象,可得a>2.5,且最大值3为y1与y2交点的纵坐标,由此联列方程组,并解之即得实数a的值.
| x+5 |
| 2 |
解答:解:令y1=
,y2=a-x2,
∵f(x)=min{
,a-x2}的最大值为3,
∴y1的图象是直线,y2的图象抛物线,且抛物线的顶点在直线y1=
上方,
由此可得a>2.5,且最大值3为y1与y2交点的纵坐标,
联列
解之得,a=4
故答案为4
| x+5 |
| 2 |

∵f(x)=min{
| x+5 |
| 2 |
∴y1的图象是直线,y2的图象抛物线,且抛物线的顶点在直线y1=
| x+5 |
| 2 |
由此可得a>2.5,且最大值3为y1与y2交点的纵坐标,
联列
|
故答案为4
点评:本题主要考查分段函数的意义,数形结合的思想以及阅读理解能力,属于中档题.结合函数的图象加以理解观察,是解决本题的关键.

练习册系列答案
相关题目
 对于任意实数a,b,定义
对于任意实数a,b,定义