Question

对于任意实数a，b，定义min{a，b}=

a，a≤b b，a＞b.

设函数f（x）=-x+3，g（x）=log₂x，则函数h（x）=min{f（x），g（x）}的最大值是

 

．

Answer 1

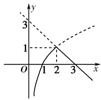
分析：分别作出函数f（x）=-3+x和g（x）=log₂x的图象，结合函数f（x）=-3+x和g（x）=log₂x的图象可知，在这两个函数的交点处函数h（x）=min{f（x），g（x）}的最大值．

解答：解：∵x＞0，∴f（x）=-x+3＜3，g（x）=log₂x∈R，分别作出函数f（x）=-3+x和g（x）=log₂x的图象，
结合函数f（x）=-3+x和g（x）=log₂x的图象可知，
h（x）=min{f（x），g（x）}的图象，
在这两个函数的交点处函数h（x）=min{f（x），g（x）}的最大值．
解方程组

y=-x+3 y=log2x

得

x=2 y=1

，
∴函数h（x）=min{f（x），g（x）}的最大值是1．
故答案是1．

点评：数形结合是求解这类问题的有效方法．