题目内容
已知函数 是定义在
是定义在 上的奇函数,且满足
上的奇函数,且满足 ,当
,当 时,
时, ,则满足
,则满足 的
的 的值是( )
的值是( )
A.
 B.
B.

C.
 D.
D.

【答案】
D
【解析】
试题分析:解:∵f(x)是奇函数且f(x+2)=-f(x),∴f(x+4)=-f(x+2)=f(x)∴函数f(x)的周期T=4.∵当0≤x≤1时,f(x)= x,又f(x)是奇函数,∴当-1≤x≤0时,f(x)=
x,又f(x)是奇函数,∴当-1≤x≤0时,f(x)= x,令
x,令 x=-
x=- 解得:x=-1,而函数f(x)是以4为周期的周期函数,∴方程f(x)=-
解得:x=-1,而函数f(x)是以4为周期的周期函数,∴方程f(x)=- 的x的值是:x=4k-1,k∈Z.故选D.
的x的值是:x=4k-1,k∈Z.故选D.
考点:函数的奇偶性和递推关系
点评:本题主要考查函数的奇偶性和递推关系,利用函数的奇偶性和周期性结合来转化是关键,属于中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。 的解析式;
的解析式; 。
。 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
, 的解析式;
的解析式;
 是定义在
是定义在 上的以5为周期的奇函数, 若
上的以5为周期的奇函数, 若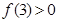 ,
, ,则a的取值范围是 ( )
,则a的取值范围是 ( )  B.
B.

 D.
D.

 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )
) ,求证:当
,求证:当 时,
时, ;
; 时,
时, 是定义在
是定义在 上的奇函数,且
上的奇函数,且
 的解析式;
的解析式; 的单调性;
的单调性;