题目内容
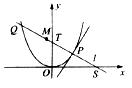
如图所示,P是抛物线C:y= x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.
x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.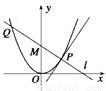
【答案】分析:设出P的坐标,过点P的切线斜率k=x,求出直线l的方程,设出Q、M坐标,利用中点坐标公式,求出m的轨迹方程,再用基本不等式求出点M到x轴的最短距离.
解答: 解:设P(x,y),则y=
解:设P(x,y),则y=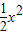 ,
,
∴过点P的切线斜率k=x,
当x=0时不合题意,∴x≠0.
∴直线l的斜率kl=-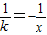 ,
,
∴直线l的方程为y-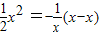 .
.
此式与y=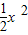 联立消去y得
联立消去y得
x2+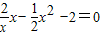
设Q(x1,y1),M(x,y).
∵M是PQ的中点,
∴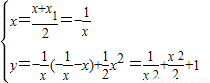
消去x,得y=x2+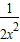 +1(x≠0)就是所求的轨迹方程.
+1(x≠0)就是所求的轨迹方程.
由x≠0知x2>0,
∴y=x2+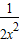 +1≥2
+1≥2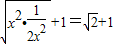
上式等号仅当x2=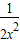 ,即x=±
,即x=±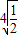 时成立,
时成立,
所以点M到x轴的最短距离是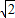 +1.
+1.
点评:本题考查直线的斜率,轨迹方程,直线与圆锥曲线的综合问题,考查学生分析问题解决问题的能力,是中档题.
解答:
 解:设P(x,y),则y=
解:设P(x,y),则y=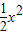 ,
,∴过点P的切线斜率k=x,
当x=0时不合题意,∴x≠0.
∴直线l的斜率kl=-
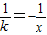 ,
,∴直线l的方程为y-
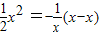 .
.此式与y=
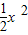 联立消去y得
联立消去y得x2+
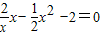
设Q(x1,y1),M(x,y).
∵M是PQ的中点,
∴
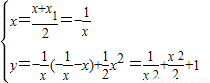
消去x,得y=x2+
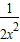 +1(x≠0)就是所求的轨迹方程.
+1(x≠0)就是所求的轨迹方程.由x≠0知x2>0,
∴y=x2+
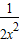 +1≥2
+1≥2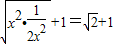
上式等号仅当x2=
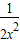 ,即x=±
,即x=±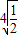 时成立,
时成立,所以点M到x轴的最短距离是
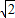 +1.
+1.点评:本题考查直线的斜率,轨迹方程,直线与圆锥曲线的综合问题,考查学生分析问题解决问题的能力,是中档题.

练习册系列答案
相关题目
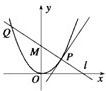 如图所示,P是抛物线C:y=
如图所示,P是抛物线C:y=