题目内容
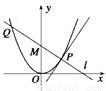
如图所示,设P是抛物线C1:x2=y上的动点,过点P作圆C2:x2+(y+3)2=1的两条切线,交直线l:y=-3于A、B两点.

(1)求圆C2的圆心M到抛物线C1准线的距离;
(2)是否存在点P,使线段AB被抛物线C1在点P处的切线平分?若存在,求出点P的坐标;若不存在,请说明理由.
(1) (2)存在点P满足题意,点P的坐标为(±
(2)存在点P满足题意,点P的坐标为(±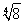 ,2
,2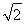 )
)
【解析】
解:(1)因为抛物线C1的准线方程为y=- ,
,
所以圆心M到抛物线C1的准线的距离为
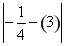 =
= .
.
(2)设点P的坐标为(x0, ),抛物线C1在点P处的切线交直线l于点D.
),抛物线C1在点P处的切线交直线l于点D.
再设A,B,D的横坐标分别为xA,xB,xD,
过点P(x0, )的抛物线C1的切线方程为
)的抛物线C1的切线方程为
y- =2x0(x-x0).①
=2x0(x-x0).①
当x0=1时,过点P(1,1)与圆C2相切的直线PA的方程为
y-1= (x-1).
(x-1).
可得xA=-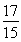 ,xB=1,xD=-1,xA+xB≠2xD.
,xB=1,xD=-1,xA+xB≠2xD.
当x0=-1时,过点P(-1,1)与圆C2相切的直线PB的方程为y-1=- (x+1),
(x+1),
可得xA=-1,xB= ,xD=1,xA+xB≠2xD,
,xD=1,xA+xB≠2xD,
所以 -1≠0.
-1≠0.
设切线PA、PB的斜率为k1,k2,
则PA:y- =k1(x-x0),②
=k1(x-x0),②
PB:y- =k2(x-x0),③
=k2(x-x0),③
将y=-3分别代入①②③得
xD= (x0≠0),
(x0≠0),
xA=x0-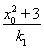 ,
,
xB=x0- (k1,k2≠0),
(k1,k2≠0),
∴xA+xB=2x0-( +3)(
+3)( +
+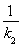 ).
).
又 =1,
=1,
即( -1)
-1)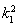 -2(
-2( +3)x0k1+(
+3)x0k1+( +3)2-1=0.
+3)2-1=0.
同理,( -1)
-1) -2(
-2( +3)x0k2+(
+3)x0k2+( +3)2-1=0.
+3)2-1=0.
∴k1、k2是方程( -1)k2-2(
-1)k2-2( +3)x0k+(
+3)x0k+( +3)2-1=0的两个不相等的根,
+3)2-1=0的两个不相等的根,
从而k1+k2= ,
,
k1·k2= .
.
因为xA+xB=2xD,
所以2x0-(3+ )(
)( +
+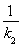 )=
)=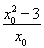 ,
,
即 +
+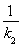 =
=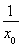 .
.
从而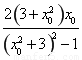 =
= ,
,
进而得 =8,
=8,
所以x0=± .
.
综上所述,存在点P满足题意,点P的坐标为(±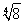 ,2
,2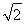 ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案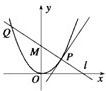 如图所示,P是抛物线C:y=
如图所示,P是抛物线C:y=
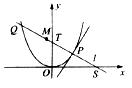
 x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.
x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.