题目内容
满足sin(2x- )≥
)≥ 的x集合是________.
的x集合是________.
[kπ+ π,kπ+
π,kπ+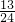 π](k∈Z)
π](k∈Z)
分析:根据正弦型函数的图象和性质,我们可以将三角不等式sin(2x- )≥
)≥ ,化为
,化为 +2kπ≤2x-
+2kπ≤2x- ≤
≤ +2kπ,k∈Z,利用不等式的性质求出x的取值范围,即可得到答案.
+2kπ,k∈Z,利用不等式的性质求出x的取值范围,即可得到答案.
解答:由正弦函数的性质
若sin(2x- )≥
)≥
则 +2kπ≤2x-
+2kπ≤2x- ≤
≤ +2kπ,k∈Z
+2kπ,k∈Z
解得kπ+ π≤x≤kπ+
π≤x≤kπ+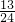 π,k∈Z
π,k∈Z
故满足sin(2x- )≥
)≥ 的x集合是[kπ+
的x集合是[kπ+ π,kπ+
π,kπ+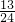 π](k∈Z)
π](k∈Z)
故答案为:[kπ+ π,kπ+
π,kπ+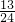 π](k∈Z)
π](k∈Z)
点评:本题考查的知识点是正弦函数的图象和性质,其中根据正弦型函数的图象和性质,将三角不等式化为关于x的一次不等式,是解答本题的关键.
 π,kπ+
π,kπ+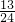 π](k∈Z)
π](k∈Z)分析:根据正弦型函数的图象和性质,我们可以将三角不等式sin(2x-
 )≥
)≥ ,化为
,化为 +2kπ≤2x-
+2kπ≤2x- ≤
≤ +2kπ,k∈Z,利用不等式的性质求出x的取值范围,即可得到答案.
+2kπ,k∈Z,利用不等式的性质求出x的取值范围,即可得到答案.解答:由正弦函数的性质
若sin(2x-
 )≥
)≥
则
 +2kπ≤2x-
+2kπ≤2x- ≤
≤ +2kπ,k∈Z
+2kπ,k∈Z解得kπ+
 π≤x≤kπ+
π≤x≤kπ+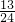 π,k∈Z
π,k∈Z故满足sin(2x-
 )≥
)≥ 的x集合是[kπ+
的x集合是[kπ+ π,kπ+
π,kπ+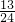 π](k∈Z)
π](k∈Z)故答案为:[kπ+
 π,kπ+
π,kπ+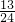 π](k∈Z)
π](k∈Z)点评:本题考查的知识点是正弦函数的图象和性质,其中根据正弦型函数的图象和性质,将三角不等式化为关于x的一次不等式,是解答本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 )≥
)≥ 的x集合是 .
的x集合是 .