题目内容
（1）求（x+2y）7展开式中系数最大的项；（2）求（x-2y）7展开式中系数最大的项.
解:（1）设r+1项系数最大，则有 即 解得 又∵0≤r≤7,∴r=5. 所以系数最大项为T6= （2）展开式中共有8项，系数最大项必为正项，即在第一、三、五、七这四项中取得.又因（x-2y）7括号内两项中后项系数绝对值大于前项系数的绝对值，故系数最大项必在中间或偏右，故只需要比较T5和T7两项系数大小即可. 点评:Tr+1与Tr+2、Tr系数的大小关系是研究系数最值的有效方法，它利用的是增减性.
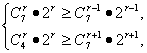
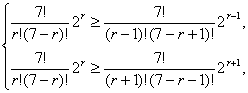
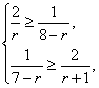
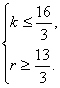
x2·25y5=672x2y5.
,所以系数最大的项是第五项，T5=
（-2y）4x3=560x3y4.
练习册系列答案
花山小状元小学生100全优卷系列答案
励耘书业试题精编系列答案
数学帮口算超级本系列答案
新新学案系列答案
勤学早好好卷系列答案
小学练习自测卷系列答案
阳光作业本课时优化设计系列答案
同步练习指导系列答案
实验指导与实验报告系列答案
通城学典周计划系列答案
相关题目
；