题目内容
(本小题满分12分)
已知函数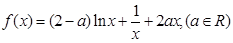
(1)当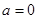 时,求
时,求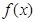 的极值;
的极值;
(2)当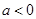 时,求
时,求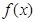 的单调区间.
的单调区间.
已知函数
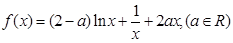
(1)当
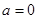 时,求
时,求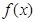 的极值;
的极值;(2)当
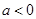 时,求
时,求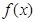 的单调区间.
的单调区间.(I)当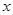 =
=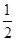 时,
时, 极小值=
极小值=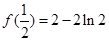 ,无极大值;
,无极大值;
(II)当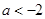 时,
时, 的单调递减区间为
的单调递减区间为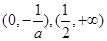
 的单调递增区间为
的单调递增区间为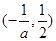
当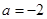 时,
时, 的单调递减区间为
的单调递减区间为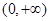
当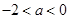 时,
时, 的单调递减区间为
的单调递减区间为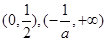
 的单调递增区间为
的单调递增区间为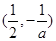 。
。
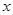 =
=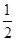 时,
时, 极小值=
极小值=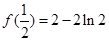 ,无极大值;
,无极大值;(II)当
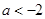 时,
时, 的单调递减区间为
的单调递减区间为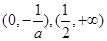
 的单调递增区间为
的单调递增区间为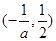
当
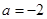 时,
时, 的单调递减区间为
的单调递减区间为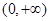
当
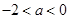 时,
时, 的单调递减区间为
的单调递减区间为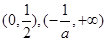
 的单调递增区间为
的单调递增区间为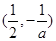 。
。(1)当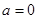 时,
时,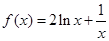 ,求导数研究单调性即可求出极值;(2)当
,求导数研究单调性即可求出极值;(2)当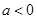 时,
时,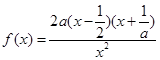 ,讨论
,讨论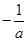 与
与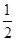 的大小可求出单调区间.
的大小可求出单调区间.
(I)当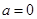 时,
时,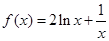
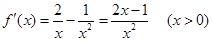 ……………………………2分
……………………………2分
………………………………4分
∴当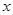 =
=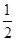 时,
时, 极小值=
极小值=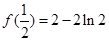 ,无极大值…………………………5分
,无极大值…………………………5分
(II)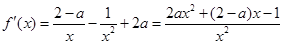
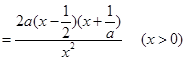 …………………………………………6分
…………………………………………6分
(1)当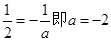 时,
时,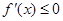 恒成立.
恒成立.
∴ 的单调递减区间为
的单调递减区间为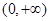 ………………………………7分
………………………………7分
(2)当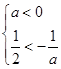 即
即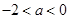 时
时
 的单调递减区间为
的单调递减区间为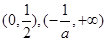
 的单调递增区间为
的单调递增区间为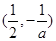 ……………………………9分
……………………………9分
(3)当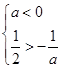 即
即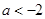 时,
时, 的单调递减区间为
的单调递减区间为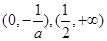
 的单调递增区间为
的单调递增区间为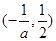 …………………………11分
…………………………11分
综上所述:当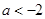 时,
时, 的单调递减区间为
的单调递减区间为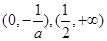
 的单调递增区间为
的单调递增区间为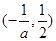
当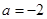 时,
时, 的单调递减区间为
的单调递减区间为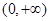
当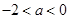 时,
时, 的单调递减区间为
的单调递减区间为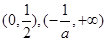
 的单调递增区间为
的单调递增区间为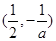 ……………………12分
……………………12分
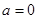 时,
时,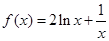 ,求导数研究单调性即可求出极值;(2)当
,求导数研究单调性即可求出极值;(2)当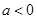 时,
时,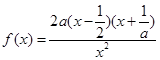 ,讨论
,讨论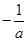 与
与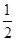 的大小可求出单调区间.
的大小可求出单调区间.(I)当
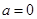 时,
时,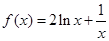
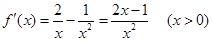 ……………………………2分
……………………………2分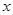 | 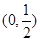 | 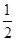 | 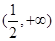 |
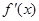 | - | 0 | + |
 | 单调递减 | 极小值 | 单调递增 |
∴当
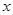 =
=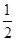 时,
时, 极小值=
极小值=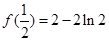 ,无极大值…………………………5分
,无极大值…………………………5分(II)
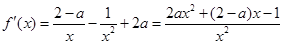
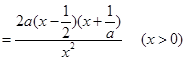 …………………………………………6分
…………………………………………6分(1)当
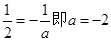 时,
时,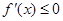 恒成立.
恒成立.∴
 的单调递减区间为
的单调递减区间为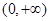 ………………………………7分
………………………………7分(2)当
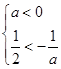 即
即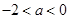 时
时 的单调递减区间为
的单调递减区间为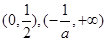
 的单调递增区间为
的单调递增区间为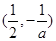 ……………………………9分
……………………………9分(3)当
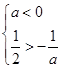 即
即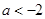 时,
时, 的单调递减区间为
的单调递减区间为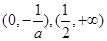
 的单调递增区间为
的单调递增区间为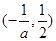 …………………………11分
…………………………11分综上所述:当
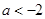 时,
时, 的单调递减区间为
的单调递减区间为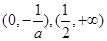
 的单调递增区间为
的单调递增区间为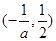
当
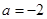 时,
时, 的单调递减区间为
的单调递减区间为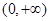
当
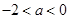 时,
时, 的单调递减区间为
的单调递减区间为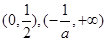
 的单调递增区间为
的单调递增区间为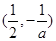 ……………………12分
……………………12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



 的定义域为
的定义域为 ,当
,当 时,
时, 是增函数,则
是增函数,则 的大小关系是____ ________________.
的大小关系是____ ________________. 是偶函数,且
是偶函数,且 上是增函数,如果
上是增函数,如果 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 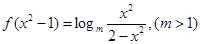 .
.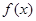 的奇偶性;
的奇偶性;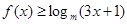 的
的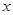 的取值范围.
的取值范围. 上为减函数的是( )
上为减函数的是( )



 在区间
在区间 上的最大值为2,求实数a的值.
上的最大值为2,求实数a的值.
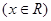 ,给出下列命题:①
,给出下列命题:①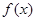 必是偶函数;②当
必是偶函数;②当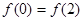 时,
时,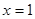 对称;③若
对称;③若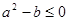 ,则
,则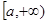 上是增函数;④
上是增函数;④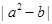 . 其中正确的命题序号是( )
. 其中正确的命题序号是( ) ,则
,则 .
.