Question

【题目】如图，三棱柱中，，分别为棱和的中点.

(1)求证:平面;

(2)若平面平面，且，求证:平面平面.

Answer 1

【答案】（1）见解析（2）见解析

【解析】分析：（1）先设的中点为，利用平几知识证得四边形为平行四边形，所以 ，再根据线面平行判定定理得结论，（2）根据等腰三角形性质得，再根据面面垂直性质定理得面，最后根据面面垂直判定定理得结论.

详解： 解：（1）如图1，设的中点为，连结，.在中，因为为的中点，所以，且，在三棱柱中，因为，且,为的中点，所以,且，所以，且,所以四边形为平行四边形，所以

又平面，平面，所以平面.

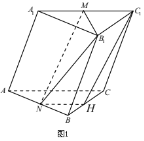
(法二)

如图2，在侧面中，连结并延长交直线于点，连结.在三棱柱中， 所以,因为为的中点，所以为中点.又因为为中点，所以,又面，面 所以平面

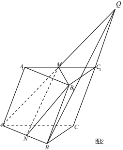
(法三)如图3，取的中点,连结、. 在中，因为、分别为、的中点，所以. 因为面，面 所以平面.在三棱柱中，且，又因为、分别为、的中点，所以，，所以四边形为平行四边形，所以,又面，面，所以面

因为面，面，，面，面，所以面面,又面,所以平面

(2)因为， 为的中点，所以，因为面面，面面，面，所以面，又面，所以面面