题目内容
已知椭圆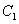 :
: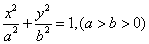 过两点
过两点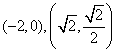 ,抛物线
,抛物线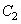 的顶点在原点,焦点在
的顶点在原点,焦点在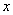 轴上,准线方程为
轴上,准线方程为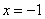 .
.
(1)求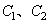 的标准方程;
的标准方程;
(2)请问是否存在直线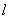 满足条件:①过
满足条件:①过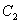 的焦点
的焦点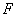 ;②与
;②与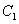 交不同两点
交不同两点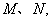 且满足直线
且满足直线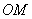 与直线
与直线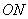 垂直?若存在,求出直线
垂直?若存在,求出直线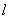 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
解:(1)把点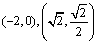 代入
代入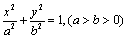 得:
得:
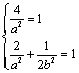 解得
解得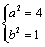 ,……………………………1分
,……………………………1分
∴椭圆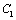 的标准方程为
的标准方程为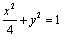 ,……………………………2分
,……………………………2分
设抛物线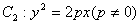 ,则有
,则有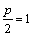 ,∴
,∴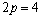 ,……………………………3分
,……………………………3分
∴抛物线的标准方程为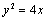 ……………………………4分
……………………………4分
(2)假设存在这样的直线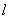 过抛物线焦点
过抛物线焦点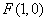 ,设直线
,设直线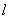 的方程为
的方程为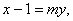
两交点坐标为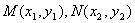 ,…………………………4分
,…………………………4分
则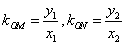 ,…………………………5分
,…………………………5分
由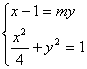 消去
消去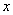 ,得
,得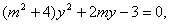 …………………………6分
…………………………6分
判别式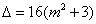 ,两根为
,两根为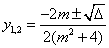
∴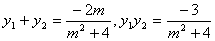 ①,…………………………7分
①,…………………………7分
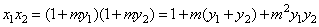 …………………………8分
…………………………8分
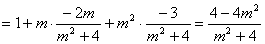 ② …………………………9分
② …………………………9分
由直线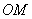 与直线
与直线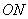 垂直,
垂直,
即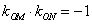 ,得
,得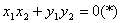 ,…………………………10分
,…………………………10分
将①②代入(*)式,得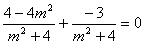 , 解得
, 解得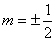 …………………11分
…………………11分
所以假设成立,即存在直线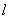 满足条件,
满足条件,
且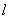 的方程为:
的方程为: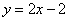 或
或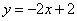 。…………………12分
。…………………12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
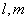 是两条不同的直线,
是两条不同的直线,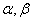 是两个不重合的平面,给出下列四个命题:
是两个不重合的平面,给出下列四个命题: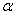 ∥
∥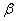 ,
,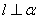 ,则
,则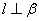 ; ②若
; ②若 ∥
∥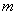 ,
,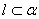 ,
,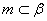 ,则
,则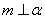 ,
,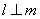 ,则
,则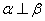 ,
, ,则
,则 的大小关系是 .
的大小关系是 . B.
B.  C.
C.  D.
D. 

 的解集为_________.
的解集为_________. 的共轭复数是( )
的共轭复数是( ) 在
在 处导数存在,则
处导数存在,则 ( )
( ) B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.

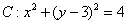 ,定直线
,定直线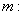
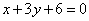 ,过
,过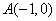 的一条动直线
的一条动直线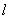 与直线
与直线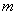 相交于
相交于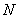 , 与圆
, 与圆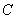 相交于
相交于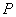 ,
,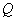 两点,
两点,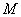 是
是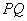 中点.
中点.  (1)当
(1)当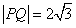 时,求直线
时,求直线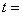
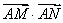 ,试问
,试问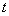 是否为定值,若为定值,请求出
是否为定值,若为定值,请求出