题目内容
已知{an}是首项为19，公差为-2的等差数列，Sn为{an}的前n项和．
(Ⅰ)求通项an及Sn；
(Ⅱ)设{bn-an}是首项为1，公比为3的等比数列，求数列{bn}的通项公式及其前n项和Tn。
(Ⅰ)求通项an及Sn；
(Ⅱ)设{bn-an}是首项为1，公比为3的等比数列，求数列{bn}的通项公式及其前n项和Tn。
解：(Ⅰ)因为{an}是首项为a1=19，公差d=-2的等差数列，
所以an=19-2(-n-1)=-2n+21，
。
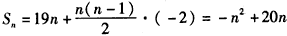(Ⅱ)由题意bn-an=3n-1，
所以bn=3n-1-2n+21，
Tn=Sn+(1+3+…+3n-1)
。
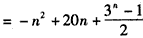所以an=19-2(-n-1)=-2n+21，
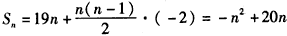。(Ⅱ)由题意bn-an=3n-1，
所以bn=3n-1-2n+21，
Tn=Sn+(1+3+…+3n-1)
。
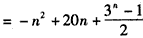练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
已知{an}是首项为1的等比数列，Sn是{an}的前n项和，且9S3=S6，则数列{
}的前5项和为（ ）
| 1 |
| an |
A、
| ||
B、
| ||
C、
| ||
D、
|