题目内容
一条直线过点P(3,2)且与x轴、y轴的正半轴分别交于A、B两点,则当S△OAB面积最小时,直线方程为________.
2x+3y-12=0
分析:设直线方程为 y-2=k(x-3),k<0,利用基本不等式可得S△OAB 最小时 k=- ,故所求直线的斜率等于-
,故所求直线的斜率等于- ,用点斜式求得直线方程.
,用点斜式求得直线方程.
解答:设直线方程为 y-2=k(x-3),k<0,可得A (3- ,0 )、B (0,2-3k),
,0 )、B (0,2-3k),
S△OAB= (3-
(3- )( 2-3k)=
)( 2-3k)= [12+(-9k)+
[12+(-9k)+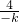 ]≥12,
]≥12,
当且仅当 (-9k)=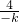 时,即 k=-
时,即 k=- 时,等号成立,
时,等号成立,
此时,直线方程为 y-2=- (x-3),即2x+3y-12=0,
(x-3),即2x+3y-12=0,
故答案为2x+3y-12=0.
点评:题考查用点斜式求直线方程的方法,基本不等式的应用,求出斜率 k=- ,是解题的关键.
,是解题的关键.
分析:设直线方程为 y-2=k(x-3),k<0,利用基本不等式可得S△OAB 最小时 k=-
 ,故所求直线的斜率等于-
,故所求直线的斜率等于- ,用点斜式求得直线方程.
,用点斜式求得直线方程.解答:设直线方程为 y-2=k(x-3),k<0,可得A (3-
 ,0 )、B (0,2-3k),
,0 )、B (0,2-3k),S△OAB=
 (3-
(3- )( 2-3k)=
)( 2-3k)= [12+(-9k)+
[12+(-9k)+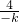 ]≥12,
]≥12,当且仅当 (-9k)=
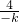 时,即 k=-
时,即 k=- 时,等号成立,
时,等号成立,此时,直线方程为 y-2=-
 (x-3),即2x+3y-12=0,
(x-3),即2x+3y-12=0,故答案为2x+3y-12=0.
点评:题考查用点斜式求直线方程的方法,基本不等式的应用,求出斜率 k=-
 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目
 轴、
轴、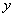 轴的正半轴分别交于A、B两点,则当
轴的正半轴分别交于A、B两点,则当 面积最小时,直线方程为____________;
面积最小时,直线方程为____________; ),且圆x2+y2=25的圆心到该直线的距离为3,则该直线的方程为( )
),且圆x2+y2=25的圆心到该直线的距离为3,则该直线的方程为( )