题目内容
一条直线过点P(3,2)且与x轴、y轴的正半轴分别交于A、B两点,则当S△OAB面积最小时,直线方程为______.
设直线方程为 y-2=k(x-3),k<0,可得A (3-
,0 )、B (0,2-3k),
S△OAB=
(3-
)( 2-3k)=
[12+(-9k)+
]≥12,
当且仅当 (-9k)=
时,即 k=-
时,等号成立,
此时,直线方程为 y-2=-
(x-3),即2x+3y-12=0,
故答案为2x+3y-12=0.
| 2 |
| k |
S△OAB=
| 1 |
| 2 |
| 2 |
| k |
| 1 |
| 2 |
| 4 |
| -k |
当且仅当 (-9k)=
| 4 |
| -k |
| 2 |
| 3 |
此时,直线方程为 y-2=-
| 2 |
| 3 |
故答案为2x+3y-12=0.

练习册系列答案
相关题目
 轴、
轴、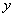 轴的正半轴分别交于A、B两点,则当
轴的正半轴分别交于A、B两点,则当 面积最小时,直线方程为____________;
面积最小时,直线方程为____________; ),且圆x2+y2=25的圆心到该直线的距离为3,则该直线的方程为( )
),且圆x2+y2=25的圆心到该直线的距离为3,则该直线的方程为( )