题目内容
一条直线过点P(-3,-
),且圆x2+y2=25的圆心到该直线的距离为3,则该直线的方程为( )
| 3 |
| 2 |
分析:分类讨论,利用点到直线的距离公式,即可得出结论.
解答:解:当直线的斜率不存在时,直线方程为x=-3,圆x2+y2=25的圆心到该直线的距离为3,满足题意;
当直线的斜率存在时,直线方程为y+
=k(x+3),即kx-y+3k-
=0,圆x2+y2=25的圆心到该直线的距离为
=3,∴k=-
,∴直线的方程为3x+4y+15=0
∴所求直线的方程为x=-3或3x+4y+15=0.
故选A.
当直线的斜率存在时,直线方程为y+
| 3 |
| 2 |
| 3 |
| 2 |
|3k-
| ||
|
| 3 |
| 4 |
∴所求直线的方程为x=-3或3x+4y+15=0.
故选A.
点评:本题考查直线方程,考查分类讨论的数学思想,考查点到直线的距离公式的运用,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 轴、
轴、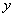 轴的正半轴分别交于A、B两点,则当
轴的正半轴分别交于A、B两点,则当 面积最小时,直线方程为____________;
面积最小时,直线方程为____________; ),且圆x2+y2=25的圆心到该直线的距离为3,则该直线的方程为( )
),且圆x2+y2=25的圆心到该直线的距离为3,则该直线的方程为( )