题目内容
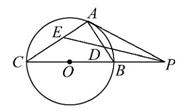
如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B,C,∠APC的平分线分别交AB,AC于点D,E.
(1)证明:∠ADE=∠AED.
(2)若AC=AP,求![]() 的值.
的值.
【解析】(1)∵PA![]() 是切线,AB是弦,∴∠BAP=∠C.
是切线,AB是弦,∴∠BAP=∠C.
又∵∠APD=∠CPE,∴∠BAP+∠APD=∠C+∠CPE.
∵∠AD![]() E=∠BAP+∠APD,∠AED=∠C+∠CPE,
E=∠BAP+∠APD,∠AED=∠C+∠CPE,
∴∠ADE=∠AED.
(2)由(1)知∠C=∠BAP,![]()
又∵∠APC=∠BPA,
∴△APC∽△BPA,∴![]() =
=![]() .
.
∵AC=AP,∴∠APC=∠C=∠BAP.
由三角形内角和定理可知,∠APC+∠C+∠CAP=180°.
∵BC是圆O的直径,∴∠BAC=90°,∴∠APC+∠C+∠BAP=180°-90°=90°,
∴∠C=30°,∴![]() =
=![]() ,∴
,∴![]() =
=![]() .
.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 (几何证明选讲选做题)
(几何证明选讲选做题)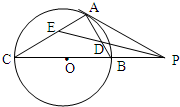 (2012•太原模拟)选修4-1:几何证明选讲
(2012•太原模拟)选修4-1:几何证明选讲 选修4-1:几何证明选讲
选修4-1:几何证明选讲 如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO点C,若圆O的半径为3,OP=5,则BC的长度
如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO点C,若圆O的半径为3,OP=5,则BC的长度 选修4-1:几何证明选讲
选修4-1:几何证明选讲