题目内容
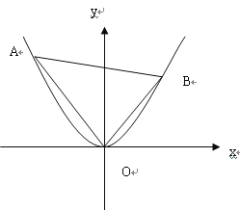
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).设
为参数).设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时,![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的普通方程;
的普通方程;
(2)设![]() 为圆
为圆![]() 上任意一点,求
上任意一点,求![]() 的最大值.
的最大值.
【答案】(1)![]() (
(![]() );(2)
);(2)![]() .
.
【解析】
(1)消元法消去参数![]() 得
得![]() 的普通方程,同理表示
的普通方程,同理表示![]() 的普通方程,最后将其消去
的普通方程,最后将其消去![]() 整理后可得答案;
整理后可得答案;
(2)由椭圆的参数方程表示其上任意点的坐标,由两点间的距离公式表示![]() ,再由三角函数求的值域确定最大值,最后开方即可.
,再由三角函数求的值域确定最大值,最后开方即可.
解法一:(1)消去参数![]() 得
得![]() 的普通方程为
的普通方程为![]() ,
,
消去参数![]() 得
得![]() 的普通方程为
的普通方程为![]() .
.
联立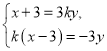 消去
消去![]() 得
得![]() ,
,
所以![]() 的普通方程为
的普通方程为![]() (
(![]() ).
).
(2)依题意,圆心![]() 的坐标为
的坐标为![]() ,半径
,半径![]() .
.
由(1)可知,![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,且
为参数,且![]() ),
),
设![]() (
(![]() ),则
),则
![]()
![]()
![]() ,
,
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
又![]() ,当且仅当
,当且仅当![]() 三点共线,且
三点共线,且![]() 在线段
在线段![]() 上时,等号成立.
上时,等号成立.
所以![]() .
.
解法二:(1)消去参数![]() 得
得![]() 的普通方程为
的普通方程为![]() ,
,
消去参数![]() 得
得![]() 的普通方程为
的普通方程为![]() .
.
由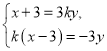 得
得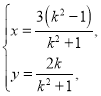
故![]() 的轨迹
的轨迹![]() 的参数方程为
的参数方程为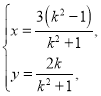 (
(![]() 为参数),
为参数),
所以![]() 的普通方程为
的普通方程为![]() (
(![]() ).
).
(2)同解法一.

练习册系列答案
相关题目