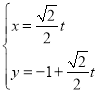题目内容
【题目】已知函数![]() .
.
(1)函数![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)函数![]() (
(![]() )的图象在点
)的图象在点![]() 处的切线为
处的切线为![]() ,证明:有且只有两个点
,证明:有且只有两个点![]() 使得直线
使得直线![]() 与函数
与函数![]() 的图象也相切.
的图象也相切.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(2)证明见解析.
上单调递增;(2)证明见解析.
【解析】
(1)先对![]() 求导,然后对a分类讨论,求出单调区间即可;
求导,然后对a分类讨论,求出单调区间即可;
(2)设![]() (
(![]() ),可求出直线
),可求出直线![]() 的方程为:
的方程为:![]() ,假设直线
,假设直线![]() 与
与![]() 的图象也相切,切点为
的图象也相切,切点为![]() ,所以直线
,所以直线![]() 的方程也可以写作为:
的方程也可以写作为:![]() ,又因为斜率相等可得
,又因为斜率相等可得![]() ,即
,即![]() ,由此可得
,由此可得![]() ,令
,令![]() (
(![]() ),然后结合零点存在性定理证明即可.
),然后结合零点存在性定理证明即可.
(1)![]() (
(![]() ),所以
),所以![]() ,
,
①当![]() 即
即![]() 时:
时:![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 即
即![]() 时:令
时:令![]() 有:
有:![]() ,
,
所以:![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增;
上单调递增;
(2)设![]() (
(![]() ),
),
![]() ,所以:
,所以:![]() ,
,
所以直线![]() 的方程为:
的方程为:![]() ,即:
,即:![]() ,①
,①
假设直线![]() 与
与![]() 的图象也相切,切点为
的图象也相切,切点为![]() ,
,
因为![]() ,所以:
,所以:![]() ,
,
所以直线![]() 的方程也可以写作为:
的方程也可以写作为:![]() ,
,
又因为![]() ,即:
,即:![]() ,
,
所以直线![]() 的方程为:
的方程为: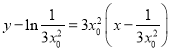 ,即:
,即:![]() ,②
,②
由①②有:![]() ,即:
,即:![]() ,
,
令![]() (
(![]() ),
),
所以![]() ,
,
令![]() ,得:
,得:![]() ,
,
所以:![]() 在
在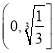 上单调递减,在
上单调递减,在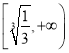 上单调递增,
上单调递增,
所以: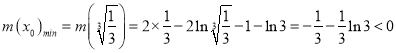 ,
,
又因为:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以:![]() 在
在![]() 有且只有两个实数根,
有且只有两个实数根,
所以有且只有两个点![]() 使得直线
使得直线![]() 与函数
与函数![]() 的图象也相切.
的图象也相切.

 期末冲刺100分创新金卷完全试卷系列答案
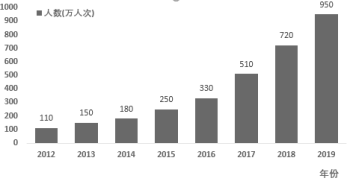
期末冲刺100分创新金卷完全试卷系列答案【题目】某蛋糕店制作并销售一款蛋糕,制作一个蛋糕成本4元,且以9元的价格出售,若当天卖不完,剩下的则无偿捐献给饲料加工厂.根据以往100天的资料统计,得到如表需求量表:
需求量/个 | [100,110) | [110,120) | [120,130) | [130,140) | [140,150] |
天数 | 15 | 25 | 30 | 20 | 10 |
该蛋糕店一天制作了这款蛋糕X(X∈N)个,以x(单位:个,100≤x≤150,x∈N)表示当天的市场需求量,T(单位:元)表示当天出售这款蛋糕获得的利润.
(1)当x=135时,若X=130时获得的利润为T1,X=140时获得的利润为T2,试比较T1和T2的大小;
(2)当X=130时,根据上表,从利润T不少于560元的天数中,按需求量分层抽样抽取6天.
(i)求此时利润T关于市场需求量x的函数解析式,并求这6天中利润为650元的天数;
(ii)再从这6天中抽取3天做进一步分析,设这3天中利润为650元的天数为ξ,求随机变量ξ的分布列及数学期望.