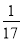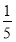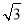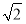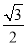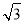题目内容
在△ABC中，a、b、c分别为角A、B、C的对边，4sin2
－cos 2A＝
.
(1)求角A的度数；
(2)若a＝
，b＋c＝3，求△ABC的面积．
（1）A＝60°.（2）
【解析】(1)∵B＋C＝π－A，即
＝
，
由4sin2－cos 2A＝
，
得4cos2
－cos 2A＝，
即2(1＋cos A)－(2cos2A－1)＝，
整理得4cos2A－4cos A＋1＝0，
即(2cos A－1)2＝0.
∴cos A＝
，又0°＜A＜180°，∴A＝60°.
(2)由A＝60°，根据余弦定理cos A＝
，得
＝
.
∴b2＋c2－bc＝3，①
又b＋c＝3，②
∴b2＋c2＋2bc＝9.③
①－③得bc＝2.④
解②④得
或
∴S△ABC＝
×1×2×sin 60°＝.
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
