题目内容
设点F1，F2为双曲线C：x2-
=1的左、右焦点，P为C为一点，若△PF1F2的面积为6，则
•
的值是（ ）
| y2 |
| 3 |
| PF1 |
| PF2 |
分析：通过三角形的面积，双曲线的定义，以及三角形△PF1F2中的余弦定理，列出关系式，求出
，
夹角的余弦值，以及两个向量模的乘积值，然后求出向量的数量积．
| PF1 |
| PF2 |
解答：解：因为双曲线C：x2-
=1所以a=1，b=
，c=2，
|PF1|-|PF2|=2a=2，⇒
2+
2-2|
|•|
|=4…①
（2c）2=
2+
2-2|
|•|
|cosθ，
即
2+
2-2|
|•|
|cosθ=16…②
又S△PF1F2=6，
|
|•|
|sinθ=6，…③
由①②③可得：2-2cosθ=sinθ，解得cosθ=1（舍去）或cosθ=
．
此时|
|•|
|=15，
则
•
=|
|•|
|cosθ=15×
=9．
故选D．
| y2 |
| 3 |
| 3 |
|PF1|-|PF2|=2a=2，⇒
| PF1 |
| PF2 |
| PF1 |
| PF2 |
（2c）2=
| PF1 |
| PF2 |
| PF1 |
| PF2 |
即
| PF1 |
| PF2 |
| PF1 |
| PF2 |
又S△PF1F2=6，
| 1 |
| 2 |
| PF1 |
| PF2 |
由①②③可得：2-2cosθ=sinθ，解得cosθ=1（舍去）或cosθ=
| 3 |
| 5 |
此时|
| PF1 |
| PF2 |
则
| PF1 |
| PF2 |
| PF1 |
| PF2 |
| 3 |
| 5 |
故选D．
点评：本题考查双曲线的基本性质，余弦定理，向量的数量积的应用，考查计算能力．
练习册系列答案
通城学典默写能手系列答案
相关题目
的左、右焦点，P为C上一点，若△PF1F2的面积为6，则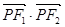
= 。
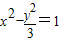的左、右焦点，P为C上一点，若△PF1F2的面积为6，则
= ．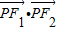