题目内容
设点F1、F2为双曲线C:x2-
=1的左、右焦点,P为C上一点,若△PF1F2的面积为6,则
•
=
| y2 |
| 3 |
| PF1 |
| PF2 |
9
9
.分析:由S△PF 1F2=
•2c|yp|=2|yp|可求|yp|代入双曲线方程可求,xp2,然后代入向量的数量积的坐标表示可求
•
| 1 |
| 2 |
| PF1 |
| PF2 |
解答:解:由题意可得,2c=F1F2=4,F1(-2,0),F2(2,0)
∵P在双曲线上
∴
-
=1
∴S△PF 1F2=
•2c|yp|=2|yp|=6
∴|yp|=3,xp2=4
则
•
=(-2-xp,-yp)•(2-xp,-yp)
=xp2-4+yp2=xp2+5=9
故答案为:9
∵P在双曲线上
∴
| xp2 |
| 1 |
| yp2 |
| 3 |
∴S△PF 1F2=
| 1 |
| 2 |
∴|yp|=3,xp2=4
则
| PF1 |
| PF2 |
=xp2-4+yp2=xp2+5=9
故答案为:9
点评:本题主要考查了向量 的数量积的坐标表示,解题的关键是双曲线的性质的应用

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 的左、右焦点,P为C上一点,若△PF1F2的面积为6,则
的左、右焦点,P为C上一点,若△PF1F2的面积为6,则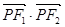 = 。
= 。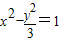 的左、右焦点,P为C上一点,若△PF1F2的面积为6,则
的左、右焦点,P为C上一点,若△PF1F2的面积为6,则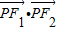 = .
= .