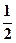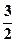题目内容
(本题满分15分)定义在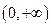 上的函数
上的函数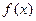 ,对任意的
,对任意的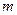 ,
,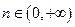 都有
都有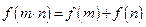 成立,且当
成立,且当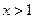 时,
时,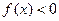 .
.
(1)试求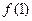 的值;
的值;
(2)证明: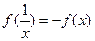 对任意
对任意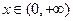 都成立;
都成立;
(3)证明: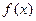 在
在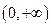 上是减函数;
上是减函数;
(4)当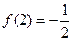 时,解不等式
时,解不等式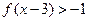 .
.
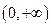 上的函数
上的函数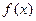 ,对任意的
,对任意的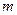 ,
,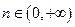 都有
都有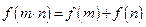 成立,且当
成立,且当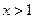 时,
时,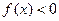 .
. (1)试求
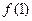 的值;
的值;(2)证明:
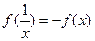 对任意
对任意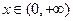 都成立;
都成立;(3)证明:
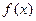 在
在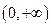 上是减函数;
上是减函数;(4)当
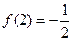 时,解不等式
时,解不等式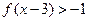 .
.(1)0
(2)证明略
(3)证明略
(4)
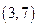
(1)∵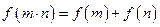 对任意的
对任意的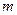 ,
,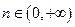 都成立,
都成立,
∴令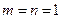 得,
得,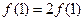 ∴
∴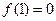 …….3分
…….3分
(2)由题意及(1)可知,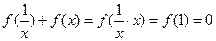
∴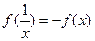 ….6分
….6分
(3)证明:任取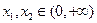 ,且
,且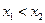 ,
,
则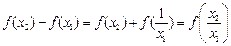 ,
,
且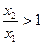 , 而当
, 而当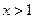 时,
时,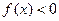 ∴
∴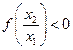 ,
,
即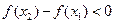 ∴
∴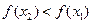 ,
,
即函数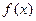 在
在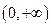 上是减函数;…….10分
上是减函数;…….10分
(4)当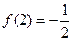 时,
时,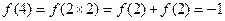
∴原不等式可化为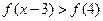 由(3)知,
由(3)知,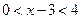
解得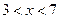 ∴原不等式
∴原不等式 的解集为
的解集为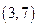 ……15分
……15分
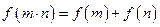 对任意的
对任意的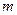 ,
,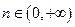 都成立,
都成立,∴令
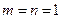 得,
得,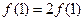 ∴
∴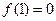 …….3分
…….3分(2)由题意及(1)可知,
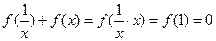
∴
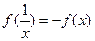 ….6分
….6分(3)证明:任取
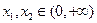 ,且
,且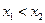 ,
,则
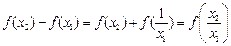 ,
,且
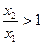 , 而当
, 而当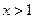 时,
时,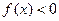 ∴
∴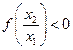 ,
,即
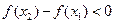 ∴
∴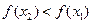 ,
,即函数
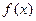 在
在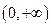 上是减函数;…….10分
上是减函数;…….10分(4)当
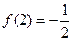 时,
时,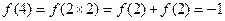
∴原不等式可化为
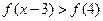 由(3)知,
由(3)知,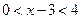
解得
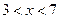 ∴原不等式
∴原不等式 的解集为
的解集为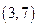 ……15分
……15分
练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
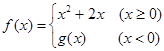 为奇函数,则
为奇函数,则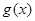 等于
等于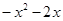
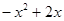
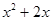
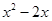
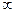 )上的增函数,且
)上的增函数,且
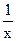 )<2.
)<2.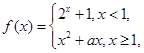 若
若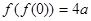 ,则实数
,则实数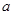 等于
等于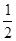
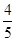
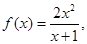
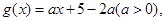 若对于任意
若对于任意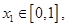 总存在
总存在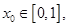 使得
使得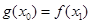 成立,则
成立,则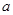 的取值范围是 ( )
的取值范围是 ( )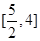
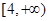
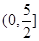
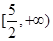
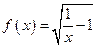 .
.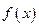 的定义域;
的定义域;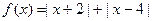 的最小值是 。
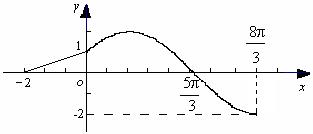
的最小值是 。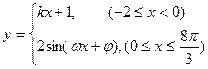 的图象如下图,则( )
的图象如下图,则( ) 



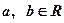 ,记
,记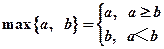 ,函数
,函数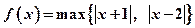
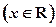 的最小值是( )
的最小值是( )