题目内容
已知f(x+1)的定义域为[0,1],则f(
)的定义域为( )
| 1 |
| x |
分析:注意y=f(x+1)与y=f(
))中的x不是同一x,但是x+1与
的范围一致,由于f(x+1)的定义域为[0,1],就是x∈[0,1],求出x+1的范围,就是函数f(
)中
的范围,从而求出x的范围,即为y=f(
)的定义域.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
解答:解:函数f(x+1)的定义域为[0,1],
所以x∈[0,1],
所以1≤x+1≤2,
对于函数f(
)
所以1≤
≤2,解得x∈[
,1],所以函数y=f(
)的定义域为:[
,1].
故选D.
所以x∈[0,1],
所以1≤x+1≤2,
对于函数f(
| 1 |
| x |
所以1≤
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 2 |
故选D.
点评:本题考查抽象函数的定义域的求法,考查计算能力,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
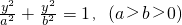 的上、下焦点及左、右顶点均在圆O:x2+y2=1上.
的上、下焦点及左、右顶点均在圆O:x2+y2=1上.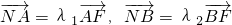 ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值.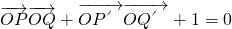 ,若点S满足:
,若点S满足: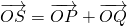 ,证明:点S在椭圆C2上.
,证明:点S在椭圆C2上. 的上、下焦点及左、右顶点均在圆O:x2+y2=1上,
的上、下焦点及左、右顶点均在圆O:x2+y2=1上, ,求证:λ1+λ2为定值;
,求证:λ1+λ2为定值; ,若点S满足:
,若点S满足: ,证明:点S在椭圆C2上。
,证明:点S在椭圆C2上。  的上、下焦点及左、右顶点均在圆O:x2+y2=1上.
的上、下焦点及左、右顶点均在圆O:x2+y2=1上. ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值. ,若点S满足:
,若点S满足: ,证明:点S在椭圆C2上.
,证明:点S在椭圆C2上. 在x=3处的切线方程为(2a-1)x-2y+3=0
在x=3处的切线方程为(2a-1)x-2y+3=0