题目内容
设an（n=2，3，4…）是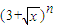
展开式中x的一次项的系数，则
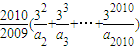的值是 ．
【答案】分析：在
展开式中令x的指数为1，得出一次项的系数即an=3n-2Cn2，根据所求式子的结构特点，先化简
=
=
=18（
），再利用裂项求和法可以求出式子的值．
解答：解：
展开式的通项为
，令
，得r=2．展开式中x的一次项的系数为3n-2Cn2，即an=3n-2Cn2 （n≥2）．
我∴
=
=
=18（
），，∴
=
×18×（1
+
+…
）=18×
×
=18×1=18
故答案为：18．
点评：本题考查二项式定理的应用、裂项法数列求和．考查转化、计算能力．得出
=18（
）是关键．
展开式中令x的指数为1，得出一次项的系数即an=3n-2Cn2，根据所求式子的结构特点，先化简===18（ ），再利用裂项求和法可以求出式子的值．解答：解：
展开式的通项为，令，得r=2．展开式中x的一次项的系数为3n-2Cn2，即an=3n-2Cn2 （n≥2）．我∴
===18（），，∴=×18×（1++…）=18××=18×1=18故答案为：18．
点评：本题考查二项式定理的应用、裂项法数列求和．考查转化、计算能力．得出
=18（ ）是关键． 
练习册系列答案
相关题目
设an（n=2，3，4，…）是(3-
)n展开式中x的一次项的系数，则
+
+…+
的值是（ ）
| x |
| 32 |
| a2 |
| 33 |
| a3 |
| 32009 |
| a2009 |
A、
| ||
B、
| ||
C、
| ||
D、
|