题目内容
如图，椭圆
上顶点为
，
为
轴正半轴上一点，
为椭圆上异于的一点，且
。
(1)若
，求
的值；
(2)若过、、
三点的圆恰好与直线
相切，求椭圆方程。
解：（1）
由椭圆离心率
，可得
，
，
由题意知
，
，所以直线
的斜率为
，
由
，得
，所以直线
的斜率为
，
设
，则
，所以
，即
，
又设
，则
，
，
由
，得
，即
，
点
在椭圆上，所以
，
将，带入上式，可得
，
所以
的值为
。
（2）设
的中点为
，则
，
，
所以过
三点的圆的圆心，半径为
，
又因为此圆与
相切，所以
，解得
，所以
，
，
椭圆方程为
。
练习册系列答案
相关题目
如图，椭圆C方程为
（
）,点
为椭圆C的左、右顶点。
与（1）中所述椭圆C相交于A、B两点（A、B不是左、右顶点），且满足
,求证：直线
过定点，并求出该点的坐标。 
,线段
的中点分别为
,且△
是面积为4的直角三角形.
做直线
交椭圆于P,Q两点,使
,求直线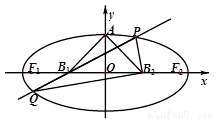
上顶点为A，Q为x轴正半轴上一点，P为椭圆上异于A的一点，且
．
的值；
+3=0相切，求椭圆方程．