题目内容
 如图,椭圆C方程为
如图,椭圆C方程为| x2 |
| a2 |
| y2 |
| b2 |
(1)若椭圆C上的点到焦点的距离的最大值为3,最小值为1,求椭圆的标准方程;
(2)若直线l:y=kx+m与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足AA2⊥BA2,求证:直线l过定点,并求出该点的坐标.
分析:(1)由题意知
,由此能求出椭圆的标准方程.
(2)设A(x1,y1),B(x2,y2),由AA2⊥BA2,知(2-x1)(2-x2)+y1y2=0.联立方程
,利用韦达定理和根的判别式能推导出7m2+16km+4k2=0,由此能够证明直线l恒过定点(
,0).
|
(2)设A(x1,y1),B(x2,y2),由AA2⊥BA2,知(2-x1)(2-x2)+y1y2=0.联立方程
|
| 2 |
| 7 |
解答:解:(1)由题意知
,
a=2,c=1,
∴椭圆的标准方程为
+
=1
(2)设A(x1,y1),B(x2,y2),
∵AA2⊥BA2,∴(2-x1)(2-x2)+y1y2=0….①
联立方程
⇒(3+4k2)x2+8kmx+4m2-12=0,
,代入①式整理,得7m2+16km+4k2=0,
所以(7m+2k)(m+2k)=0
当7m=-2k时,满足△>0.此时,直线l:y=-
mx+m恒过点(
,0)
当m=-2k时,满足△>0.此时,直线l:y=-
mx+m恒过点(2,0)不符合题意,舍.
所以,直线l恒过定点(
,0).
|
a=2,c=1,
∴椭圆的标准方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设A(x1,y1),B(x2,y2),
∵AA2⊥BA2,∴(2-x1)(2-x2)+y1y2=0….①
联立方程
|
|
所以(7m+2k)(m+2k)=0
当7m=-2k时,满足△>0.此时,直线l:y=-
| 7 |
| 2 |
| 2 |
| 7 |
当m=-2k时,满足△>0.此时,直线l:y=-
| 1 |
| 2 |
所以,直线l恒过定点(
| 2 |
| 7 |
点评:本题考查椭圆方程的求法,考查直线恒过定点的证明,解题时要认真审题,注意韦达定理、根的判别式、分类讨论思想的合理运用.

练习册系列答案
相关题目
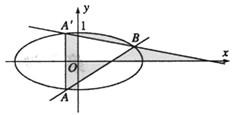 如图,椭圆
如图,椭圆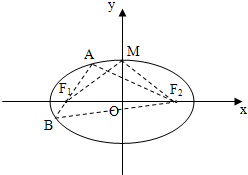 如图,椭圆C的中心在原点,焦点在x轴上,F1,F2分别是椭圆C的左、右焦点,M是椭圆短轴的一个端点,过F1的直线l与椭圆交于A,B两点,△MF1F2的面积为4,△ABF2的周长为
如图,椭圆C的中心在原点,焦点在x轴上,F1,F2分别是椭圆C的左、右焦点,M是椭圆短轴的一个端点,过F1的直线l与椭圆交于A,B两点,△MF1F2的面积为4,△ABF2的周长为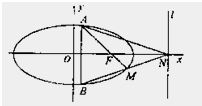 如图,椭圆
如图,椭圆 如图,椭圆C:
如图,椭圆C: (2013•江西)如图,椭圆C:
(2013•江西)如图,椭圆C: