题目内容
设同时满足条件:①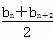 ≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
(1) 若数列{an}为等差数列,Sn是其前n项和,a3=4,S3=18,求Sn;
(2) 判断(1)中的数列{Sn}是否为“特界” 数列,并说明理由.
解:(1) 设等差数列{an}的公差为d,
则a1+2d=4,3a1+3d=18,解得a1=8,d=-2,Sn=na1+ =-n2+9n.
=-n2+9n.
(2) 由 -Sn+1=
-Sn+1=
= =
=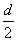 =-1<0,得
=-1<0,得 <Sn+1,故数列{Sn}适合条件①,而Sn=-n2+9n=-
<Sn+1,故数列{Sn}适合条件①,而Sn=-n2+9n=- (n∈N*),则当n=4或5时,Sn有最大值20.即Sn≤20,故数列{Sn}适合条件②.
(n∈N*),则当n=4或5时,Sn有最大值20.即Sn≤20,故数列{Sn}适合条件②.
综上,数列{Sn}是“特界”数列.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +y2=1上,顶点A与椭圆的焦点F1重合,且椭圆的另外一个焦点F2在BC边上,则△ABC的周长是________.
+y2=1上,顶点A与椭圆的焦点F1重合,且椭圆的另外一个焦点F2在BC边上,则△ABC的周长是________. =1的渐近线方程为________.
=1的渐近线方程为________. ,且∠ABC=120°,BC=10,边BC在x轴上且y轴垂直平分BC边,则过点A且以B、C为焦点的双曲线方程为______________.
,且∠ABC=120°,BC=10,边BC在x轴上且y轴垂直平分BC边,则过点A且以B、C为焦点的双曲线方程为______________. ×底×高,可得扇形的面积公式为________.
×底×高,可得扇形的面积公式为________. ”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ .
”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ . ”时,假设的内容应为______________.
”时,假设的内容应为______________. +
+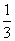 +…+
+…+ (n∈N),则n=1时,f(n)=________.
(n∈N),则n=1时,f(n)=________. 中,已知
中,已知 ,则
,则 等于
等于 (B)
(B) (C)
(C) (D)
(D)