题目内容
 椭圆C:
椭圆C: =1(a>b>0)的离心率
=1(a>b>0)的离心率 ,a+b=3.
,a+b=3.(1)求椭圆C的方程;
(2)如图,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意点,直线DP交x轴于点N直线AD交BP于点M,设BP的斜率为k,MN的斜率为m,证明2m-k为定值.
【答案】分析:(1)由题目给出的离心率及a+b=3,结合条件a2=b2+c2列式求出a,b,则椭圆方程可求;
(2)设出直线方程,和椭圆方程联立后解出P点坐标,两直线方程联立解出M点坐标,由D,P,N三点共线解出N点坐标,
由两点求斜率得到MN的斜率m,代入2m-k化简整理即可得到2m-k为定值.
解答:(1)解:因为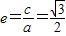 ,所以
,所以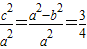 ,即a2=4b2,a=2b.
,即a2=4b2,a=2b.
又a+b=3,得a=2,b=1.
所以椭圆C的方程为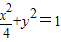 ;
;
(2)证明:因为B(2,0),P不为椭圆顶点,则可设直线BP的方程为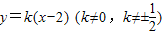 .
.
联立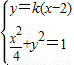 ,得(4k2+1)x2-16k2x+16k2-4=0.
,得(4k2+1)x2-16k2x+16k2-4=0.
所以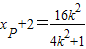 ,
,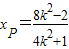 .
.
则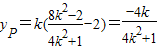 .
.
所以P(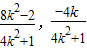 ).
).
又直线AD的方程为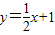 .
.
联立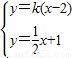 ,解得M(
,解得M(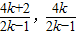 ).
).
由三点D(0,1),P(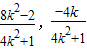 ),N(x,0)共线,
),N(x,0)共线,
得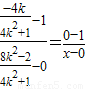 ,所以N(
,所以N(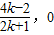 ).
).
所以MN的斜率为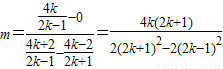 =
=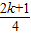 .
.
则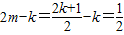 .
.
所以2m-k为定值 .
.
点评:本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,训练了二次方程中根与系数关系,考查了由两点求斜率的公式,是中高档题.
(2)设出直线方程,和椭圆方程联立后解出P点坐标,两直线方程联立解出M点坐标,由D,P,N三点共线解出N点坐标,
由两点求斜率得到MN的斜率m,代入2m-k化简整理即可得到2m-k为定值.
解答:(1)解:因为
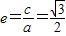 ,所以
,所以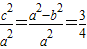 ,即a2=4b2,a=2b.
,即a2=4b2,a=2b.又a+b=3,得a=2,b=1.
所以椭圆C的方程为
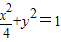 ;
;(2)证明:因为B(2,0),P不为椭圆顶点,则可设直线BP的方程为
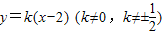 .
.联立
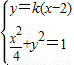 ,得(4k2+1)x2-16k2x+16k2-4=0.
,得(4k2+1)x2-16k2x+16k2-4=0.所以
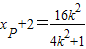 ,
,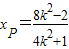 .
.则
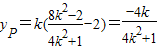 .
.所以P(
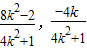 ).
).又直线AD的方程为
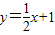 .
.联立
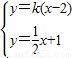 ,解得M(
,解得M(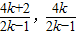 ).
).由三点D(0,1),P(
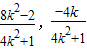 ),N(x,0)共线,
),N(x,0)共线,得
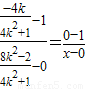 ,所以N(
,所以N(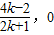 ).
).所以MN的斜率为
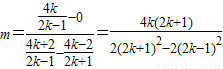 =
=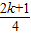 .
.则
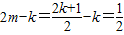 .
.所以2m-k为定值
 .
.点评:本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,训练了二次方程中根与系数关系,考查了由两点求斜率的公式,是中高档题.

练习册系列答案
相关题目
 =1(a>b>0)的离心率
=1(a>b>0)的离心率 ,直线
,直线 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切. ,-l).
,-l). +
+ =1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e.
=1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e. ,且恰好经过椭圆的右顶点,求e的大小;
,且恰好经过椭圆的右顶点,求e的大小; y+3=0相切,求椭圆方程.
y+3=0相切,求椭圆方程.
 +
+ =1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e.
=1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e. ,且恰好经过椭圆的右顶点,求e的大小;
,且恰好经过椭圆的右顶点,求e的大小; y+3=0相切,求椭圆方程.
y+3=0相切,求椭圆方程.
 =1(a>b>0)的左、右两个焦 点。(1)若椭圆C上的点A(1,
=1(a>b>0)的左、右两个焦 点。(1)若椭圆C上的点A(1, )到F1、F2两点的 距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的 距离之和等于4,写出椭圆C的方程和焦点坐标; =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为
 :
: 与
与 轴交于点T,P为
轴交于点T,P为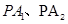 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.