题目内容

已知M(1+cos2x，1)，N(1，
3
sin2x+a)（x∈R，a是常数），且y=
OM
•
ON
（O是坐标原点）．
（1）求y关于x的函数关系式y=f（x）；
（2）若x∈[0，
π
2
]，f（x）的最大值为4，求a的值；若此时f（x）的图象可由 y=2sin2x的图象按向量
m
平移得到，求向量
m
．
分析：（1）由题意可得y=f（x）=
OM
•
ON
=1+cos2x+
3
sin2x+a，在利用两角和的正弦公式化为 2sin（2x+
π
6
）+a+1．
（2）由x∈[0，
π
2
]，利用正弦函数的定义域和值域求得f（x）的最大值为2+a+1=4，可得a=1．再根据函数y=Asin（ωx+φ）的周期性以及图象变换规律，
求得向量
m
的坐标．
解答：解：（1）由题意可得y=f（x）=
OM
•
ON
=1+cos2x+
3
sin2x+a=2sin（2x+
π
6
）+a+1．
（2）由x∈[0，
π
2
]，可得2x+
π
6
∈[
π
6
，
7π
6
]，∴2sin（2x+
π
6
）∈[-1，2]，
故f（x）的最大值为2+a+1=4，a=1．
∴f（x）=2sin（2x+
π
6
）+2=2sin2（x+
π
12
）+2的周期为π，故把y=2sin2x的图象按照向量
m
=（kπ-
π
12
，2）平移可得．
点评：本题主要考查两个向量的数量积公式，两角和差的正弦公式的应用，函数y=Asin（ωx+φ）的图象变换规律，属于中档题．
练习册系列答案
相关题目
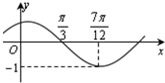精英家教网已知函数f（x）=Msin（ωx+φ）（其中M＞0，ω＞0，|φ|＜
π
2
）的图象如图所示．
（1）求函数f（x）的表达式；
（2）设α∈(
π
6
，  
2π
3
)，  β∈(-
5π
6
，-
π
3
)，  f(
α
2
)=
3
5
，  f(
β
2
)=-
4
5
，求cos2（α-β）的值．
已知集合A={x|x=cos2
(2n-1)πm
，n∈Z}，当m为4022时，集合A的元素个数为
 
．
已知f(x)=cos2x+2
3
sinxcosx．
（1）求函数f（x）的最大值M，最小正周期T．
（2）若f(α)=
8
5
，求cos2α的值．
（1）求值sin2120°+cos180°+tan45°-cos2（-330°）+sin（-210°）
（2）化简：
sin(α-
π
2
)cos(α+
3π
2
)tan(π-α)
tan(-π-α)sin(-π-α)

（3）已知tanα=m，求sinα、cosα．

已知．

        (1)求函数f(x)的最大值M，最小正周期T．

(2)若，求cos2α的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网