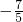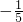Question

设a是第四象限角，sina=-

3

5

，则

2

cos（a+

π

4

）=（　　）

• A、

  7

  5

• B、

  1

  5

• C、-

  7

  5

• D、-

  1

  5

Answer 1

分析：求cosα，利用两角差的余弦公式把要求的式子展开，用特殊角的三角函数值把式子化为cosα-sinα，代入数值求解．

解答：解：∵a是第四象限角，sina=-

3

5

，∴cosa=

4

5

，

2

cos（α+

π

4

）=

2

（cosαcos

π

4

-sinαsin

π

4

）
=cosα-sinα=

4

5

+

3

5

=

7

5

．
故选A．

点评：本题涉及到平方关系，两角差的余弦公式，特殊角的三角函数值，是运用基础知识进行基本运算的题目，属基础题．