题目内容
(本小题满分10分)在 中,内角
中,内角 所对的边分别为
所对的边分别为 ,若
,若 .
.
(1)求证: 成等比数列;(2)若
成等比数列;(2)若 ,求
,求 的面积
的面积 .
.
(1)见解析;(2)
【解析】
试题分析:(1)第一步首先利用切化弦,整理后的正弦式借助正弦定理进行角化边即可得出结论,第二步借助第一步结论,把 代入得:
代入得: ,利用余弦定理求出
,利用余弦定理求出
 ,最后求面积.
,最后求面积.
试题解析:(1)由已知 .得:
.得: ,
,
即: ,即:
,即:
由正弦定理: ,所以:
,所以: 成等比数列.
成等比数列.
(2)由(1)知: ,
, ,所以:
,所以: ,
,
由余弦定理: ,所以:
,所以:
所以:
考点:1.三角函数的切化弦;2.正弦定理;3.余弦定理;4.三角形的面积公式;
考点分析: 考点1:解三角形 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 ,点
,点 ,以线段AB为直径的圆内切于圆
,以线段AB为直径的圆内切于圆 ,记点B的轨迹为
,记点B的轨迹为 .
.
 的方程;
的方程; ,则抛物线的标准方程是( )
,则抛物线的标准方程是( ) B.
B. C.
C. D.
D.
 为等比数列,若
为等比数列,若 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,
,
 是
是 上的增函数;
上的增函数; ,当
,当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围. ,若方程
,若方程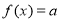 有四个不同的解
有四个不同的解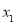 ,
,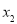 ,
,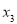 ,
,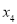 ,且
,且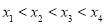 ,则
,则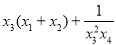 的取值范围是( )
的取值范围是( )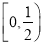 B.
B.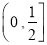 C.
C.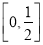 D.
D.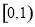
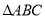 中 “
中 “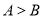 ”是“
”是“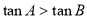 ”的( )
”的( )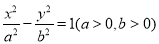 的一个焦点到一条渐近线的距离为
的一个焦点到一条渐近线的距离为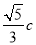 (
(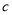 为双曲线的半焦距长),则双曲线的离心率为( )
为双曲线的半焦距长),则双曲线的离心率为( )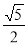 B.
B.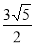 C.
C.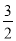 D.
D.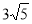
 中,含
中,含 项的系数为 .
项的系数为 .