题目内容
6.已知复数z=-1+i,则复数$\frac{z+3}{\overline z+2}$的模为( )| A. | $\sqrt{10}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
分析 把z代入$\frac{z+3}{\overline z+2}$,利用复数代数形式的乘除运算化简,再由复数模的计算公式求解.
解答 解:∵z=-1+i,
∴$\frac{z+3}{\overline z+2}$=$\frac{-1+i+3}{-1-i+2}=\frac{2+i}{1-i}$=$\frac{(2+i)(1+i)}{(1-i)(1+i)}=\frac{1+3i}{2}=\frac{1}{2}+\frac{3}{2}i$,
∴复数$\frac{z+3}{\overline z+2}$的模为$\sqrt{\frac{1}{4}+\frac{9}{4}}=\frac{\sqrt{10}}{2}$.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
16. 如图在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点.在A、P、M、C中任取一点记为E,在B、Q、N、D中任取一点记为F.设G为满足向量$\overrightarrow{OG}$=$\overrightarrow{OE}$+$\overrightarrow{OF}$的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为( )
如图在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点.在A、P、M、C中任取一点记为E,在B、Q、N、D中任取一点记为F.设G为满足向量$\overrightarrow{OG}$=$\overrightarrow{OE}$+$\overrightarrow{OF}$的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为( )
 如图在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点.在A、P、M、C中任取一点记为E,在B、Q、N、D中任取一点记为F.设G为满足向量$\overrightarrow{OG}$=$\overrightarrow{OE}$+$\overrightarrow{OF}$的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为( )
如图在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点.在A、P、M、C中任取一点记为E,在B、Q、N、D中任取一点记为F.设G为满足向量$\overrightarrow{OG}$=$\overrightarrow{OE}$+$\overrightarrow{OF}$的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为( )| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
16.已知定义在R上的函数f(x)=x2+2ax+3在(-∞,1]上是减函数,当x∈[a+1,1]时,f(x)的最大值与最小值之差为g(a),则g(a)的最小值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
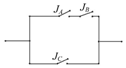 如图,JA,JB两个开关串联再与开关JC并联,在某段时间内每个开关能够闭合的概率都是0.5,计算在这段时间内线路正常工作的概率为0.625.
如图,JA,JB两个开关串联再与开关JC并联,在某段时间内每个开关能够闭合的概率都是0.5,计算在这段时间内线路正常工作的概率为0.625.