题目内容
若a＜b＜0，则下列结论不成立的是（ ）A．
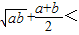
B．
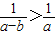
C．|a|＞|b|
D．
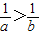
【答案】分析：根据不等式的性质和基本不等式加以证明，可得A、C、D都可以证明它们的正确性，而B项可通过举出反例得到它不成立．由此可得本题答案．
解答：解：对于A，因为a＜b＜0，可得-a＞-b＞0
所以（-a）+（-b）≥2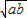
，并且等号不等式立
∴-
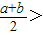
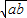，可得
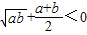，A项成立；
对于B，当a=-3，b=-2时，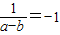
，
=-
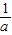不能满足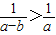
，故B项不成立；
对于C，因为a＜b＜0，所以-a＞-b＞0，
结合|a|=-a，|b|=-b，可得|a|＞|b|；
对于D，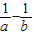
=
，
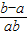因为a＜b＜0，得b-a＞0，且ab＞0．
所以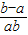
＞0，故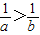
，可得D项成立
故选：B
点评：本题给出a＜b＜0，叫我们判断几个关于a、b的不等式的正确与否．着重考查了不等式的性质和基本不等式等知识，属于基础题．
解答：解：对于A，因为a＜b＜0，可得-a＞-b＞0
所以（-a）+（-b）≥2
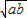，并且等号不等式立∴-
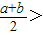
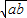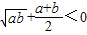，可得，A项成立；对于B，当a=-3，b=-2时，
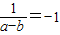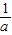，=-不能满足
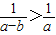，故B项不成立；对于C，因为a＜b＜0，所以-a＞-b＞0，
结合|a|=-a，|b|=-b，可得|a|＞|b|；
对于D，
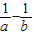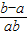=，因为a＜b＜0，得b-a＞0，且ab＞0．
所以
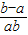＞0，故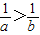，可得D项成立故选：B
点评：本题给出a＜b＜0，叫我们判断几个关于a、b的不等式的正确与否．着重考查了不等式的性质和基本不等式等知识，属于基础题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目