题目内容
已知点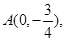 点
点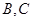 分别是
分别是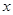 轴和
轴和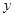 轴上的动点,且
轴上的动点,且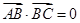 ,动点
,动点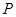 满足
满足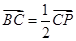 ,设动点
,设动点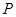 的轨迹为E.
的轨迹为E.
(1)求曲线E的方程;
(2)点Q(1,a),M,N为曲线E上不同的三点,且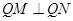 ,过M,N两点分别作曲线E的切线,记两切线的交点为
,过M,N两点分别作曲线E的切线,记两切线的交点为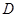 ,求
,求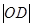 的最小值.
的最小值.
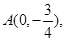 点
点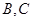 分别是
分别是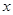 轴和
轴和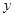 轴上的动点,且
轴上的动点,且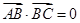 ,动点
,动点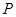 满足
满足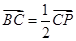 ,设动点
,设动点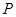 的轨迹为E.
的轨迹为E.(1)求曲线E的方程;
(2)点Q(1,a),M,N为曲线E上不同的三点,且
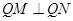 ,过M,N两点分别作曲线E的切线,记两切线的交点为
,过M,N两点分别作曲线E的切线,记两切线的交点为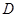 ,求
,求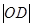 的最小值.
的最小值.(1)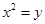 ;(2)
;(2)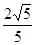 .
.
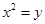 ;(2)
;(2)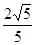 .
.试题分析:(1)设
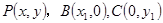 ,利用
,利用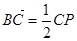 ,用
,用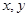 表示
表示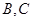 的坐标,然后利用
的坐标,然后利用 ,得到
,得到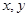 的方程,得到
的方程,得到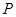 点轨迹;
点轨迹;(2)解法一:利用曲线方程
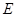 ,求出
,求出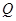 点坐标,设
点坐标,设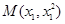 ,
,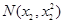 ,
,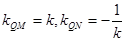 ,通过联立方程,得到
,通过联立方程,得到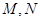 的坐标,利用导数,列出过点
的坐标,利用导数,列出过点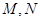 的切线方程,解出点
的切线方程,解出点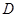 的坐标,然后再求
的坐标,然后再求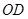 的最小值,
的最小值,解法二:利用导数,列出过点
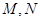 的切线方程,解出点
的切线方程,解出点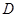 的坐标,然后结合
的坐标,然后结合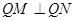 ,能够得到关于点
,能够得到关于点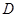 所满足的方程,再求出
所满足的方程,再求出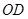 的最小值.
的最小值.试题解析:(1)解:设
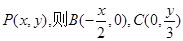
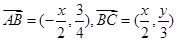 ,由
,由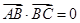 得
得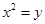 4分
4分(2)解法一:易知
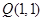 ,设
,设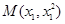 ,
,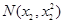 ,
,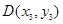 ,
,设
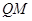 的方程为
的方程为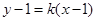
联立方程
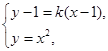 消去
消去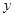 ,得
,得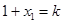 ,所以
,所以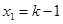 .
.同理,设
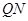 的方程为
的方程为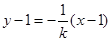 ,
,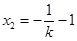 . 6分
. 6分对函数
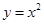 求导,得
求导,得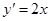 ,
,所以抛物线
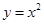 在点
在点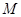 处的切线斜率为
处的切线斜率为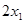 ,
,所以切线
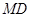 的方程为
的方程为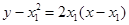 ,即
,即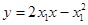 .
.同理,抛物线
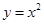 在点
在点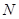 处的切线
处的切线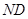 的方程为
的方程为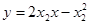 . 8分
. 8分联立两条切线的方程
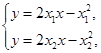
解得
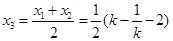 ,
,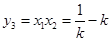 ,
,所以点
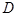 的坐标为
的坐标为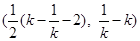 .因此点
.因此点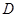 在直线
在直线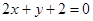 上. 10分
上. 10分因为点
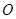 到直线
到直线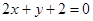 的距离
的距离 ,
,所以
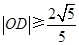 ,当且仅当点
,当且仅当点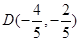 时等号成立.
时等号成立.由
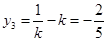 ,得
,得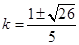 ,验证知符合题意.
,验证知符合题意.所以当
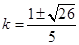 时,
时,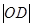 有最小值
有最小值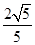 . 12分
. 12分解法二:由题意,
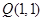 ,设
,设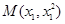 ,
,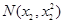 ,
,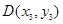 ,
,对函数
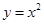 求导,得
求导,得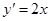 ,
,所以抛物线
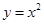 在点
在点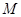 处的切线斜率为
处的切线斜率为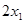 ,
,所以切线
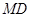 的方程为
的方程为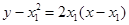 ,即
,即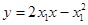 .
.同理,抛物线
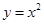 在点
在点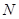 处的切线
处的切线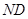 的方程为
的方程为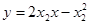 .
.联立两条切线的方程
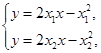
解得
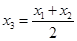 ,
,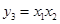 , 8分
, 8分又
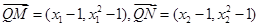
由
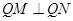 得
得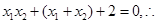
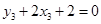
所以点
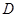 在直线
在直线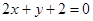 上 10分
上 10分因为点
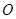 到直线
到直线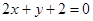 的距离
的距离 ,
,所以
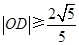 ,当且仅当点
,当且仅当点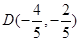 时等号成立.
时等号成立.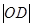 有最小值
有最小值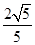 . 12分
. 12分
练习册系列答案
相关题目
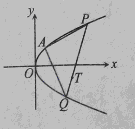
 ,求点A的坐标;
,求点A的坐标;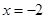 ,则抛物线的方程是( )
,则抛物线的方程是( )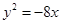
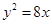
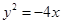
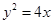
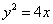 的焦点到双曲线
的焦点到双曲线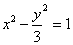 的渐近线的距离是( )
的渐近线的距离是( )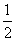

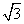
 上一点,设P到此抛物线准线的距离是
上一点,设P到此抛物线准线的距离是 ,到直线
,到直线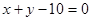 的距离是
的距离是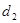 ,则
,则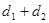 的最小值是
的最小值是 的焦点在直线
的焦点在直线 上,则
上,则 _____;
_____; 的准线方程为_____.
的准线方程为_____. 的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且
的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且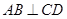 ,则
,则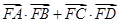 的最大等于 ( )
的最大等于 ( )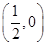 的距离比到y轴的距离大
的距离比到y轴的距离大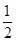 .记点P的轨迹为曲线C.
.记点P的轨迹为曲线C.