题目内容
【题目】已知二次函数![]() 对任意实数
对任意实数![]() ,都有
,都有![]() 恒成立.
恒成立.
(Ⅰ)证明: ![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 的表达式;
的表达式;
(Ⅲ)在题(Ⅱ)的条件下设![]() ,若
,若![]() 图象上的点都位于直线
图象上的点都位于直线![]() 的上方,求实数
的上方,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】试题分析:(1)令![]() 即可得解;
即可得解;
(2)由![]() ,
, ![]() 求得
求得![]() ,即
,即![]() ,再由二次不等式恒成立的条件为
,再由二次不等式恒成立的条件为![]() >0,判别式非正,即可得到
>0,判别式非正,即可得到![]() ,c,进而得到解析式;
,c,进而得到解析式;
(3)由题意知![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,结合二次函数判别式求解即可.
上恒成立,结合二次函数判别式求解即可.
试题解析:
(Ⅰ)证明:由题意可得![]() ,则
,则![]() ;
;
(Ⅱ)由(Ⅰ)知: ![]() ,即
,即![]() ,
,
又![]() ,即
,即![]() ,
,
两式相减可得: ![]() ,即
,即![]() ,
,
所以![]() ,
,
对任意实数![]() ,都有
,都有![]() ,即为
,即为![]() 恒成立,
恒成立,
则有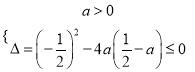 ,化简得
,化简得 ,
,
所以![]() ,
,
所以![]() ,经检验,符合题意.
,经检验,符合题意.
(Ⅲ)由题意知![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,即
上恒成立,即![]() .
.
(ⅰ)由![]() ,即
,即![]() ,解得
,解得![]() ;
;
(ⅱ)由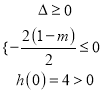 ,解得
,解得![]() ,综上可知,
,综上可知, ![]() .
.
法2:由题意知![]() 在
在![]() 上恒成立.
上恒成立.
(ⅰ)当![]() 时,
时, ![]() 成立;
成立;
(ⅱ)当![]() 时,
时, ![]() 在
在![]() 上恒成立,又当
上恒成立,又当![]() 时,
时, ![]() (当且仅当
(当且仅当![]() 时取得最小值),所以
时取得最小值),所以![]() ,解得
,解得![]() .
.
点集:解决不等式恒成立问题的“两种”常用方法
(1)分离参数法:将原不等式分离参数,转化为不含参数的函数的最值问题,利用导数求该函数的最值,根据要求得所求范围.一般地,f(x)≥a恒成立,只需![]() 即可;
即可; ![]() 恒成立,只需
恒成立,只需![]() 即可.
即可.
(2)函数思想法:将不等式转化为某含待求参数的函数的最值问题,利用导数求该函数的极值(最值),然后构建不等式求解.

 阅读快车系列答案
阅读快车系列答案【题目】长春市的“名师云课”活动自开展以来获得广大家长和学生的高度赞誉,在我市推出的第二季名师云课中,数学学科共计推出36节云课,为了更好地将课程内容呈现给学生,现对某一时段云课的点击量进行统计:
点击量 |
|
|
|
节数 | 6 | 18 | 12 |
(Ⅰ)现从36节云课中采用分层抽样的方式选出6节,求选出的点击量超过3000的节数.
(Ⅱ)为了更好地搭建云课平台,现将云课进行剪辑,若点击量在区间![]() 内,则需要花费40分钟进行剪辑,若点击量在区间
内,则需要花费40分钟进行剪辑,若点击量在区间![]() 内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中随机取出2节课进行剪辑,求剪辑时间
内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中随机取出2节课进行剪辑,求剪辑时间![]() 的分布列与数学期望.
的分布列与数学期望.