题目内容
设 .
.
(1)求函数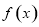 的图象在点
的图象在点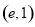 处的切线方程;
处的切线方程;
(2)求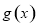 的单调区间;
的单调区间;
(3)当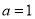 时,求实数
时,求实数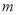 的取值范围,使得
的取值范围,使得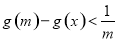 对任意
对任意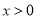 恒成立.
恒成立.
(1)切线方程为:x-ey=0;(2)当a≤0时,g(x)在(0,+∞)上单调递增;当a>0时,g(x)在(0,a)上单调递减,在(a,+∞)上单调递增;(3)0<m<e.
【解析】
试题分析:(1)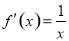 , 1分
, 1分
由导数的几何意义可知,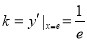 ,
,
所以切线的方程为: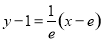 ,即x-ey=0; 3分
,即x-ey=0; 3分
(2)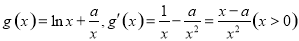 , 4分
, 4分
当a≤0时,在(0,+∞)上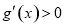 ,此时g(x)在(0,+∞)上单调递增;
,此时g(x)在(0,+∞)上单调递增;
当a>0时,在(0,a)上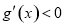 ,此时g(x)在(0,a)上单调递减,在(a,+∞)上
,此时g(x)在(0,a)上单调递减,在(a,+∞)上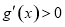 ,此时g(x) 在(a,+∞)上单调递增; 7分
,此时g(x) 在(a,+∞)上单调递增; 7分
综上所述:当a≤0时,g(x)在(0,+∞)上单调递增;当a>0时,g(x)在(0,a)上单调递减,在(a,+∞)上单调递增; 8分
(3)当a=1时,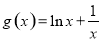 ,不等式为
,不等式为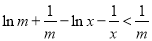 ,即
,即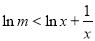 ,只需lnm小于
,只需lnm小于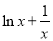 的最小值即可. 10分
的最小值即可. 10分
由(2)可知,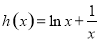 在(0,1)上单调递减,在(1,+∞)上单调递增,
在(0,1)上单调递减,在(1,+∞)上单调递增,
∴当x=1时,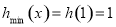 . 12分
. 12分
故lnm<1,可得0<m<e,∴m的取值范围是0<m<e. 13分
考点:考查了导数的几何意义,利用导数研究函数的单调性及最值.

练习册系列答案
相关题目
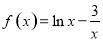 在区间
在区间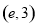 上有且只有一个零点;
上有且只有一个零点; 是两个不同的平面.若
是两个不同的平面.若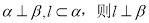 ;
;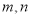 表示两条不同直线,
表示两条不同直线,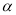 表示平面.若
表示平面.若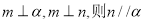 ;
;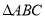 中,已知
中,已知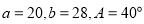 ,在求边c的长时有两解.
,在求边c的长时有两解. (其中
(其中 ),若
),若 ,则
,则 在同一坐标系内的大致图象是
在同一坐标系内的大致图象是
 在点
在点 处的切线与直线
处的切线与直线 垂直,则
垂直,则 ————.
————. 的各项均为正数,且
的各项均为正数,且 ,则
,则 .
.