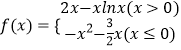Question

【题目】在△ABC中， ，其面积为 ，则tan2Asin2B的最大值是 ．

Answer 1

【答案】3﹣2
【解析】解：△ABC中， ， ∴bacos（π﹣C）=﹣bacosC=2 ，
∴abcosC=﹣2 ；
又三角形的面积为 absinC= ，
∴absinC=2 ；
∴sinC=﹣cosC，
∴C= ，
∴A+B= ；
∴tan2Asin2B=tan2Asin2（ ﹣A）
=tan2Acos2A
=tan2A（cos2A﹣sin2A）
=tan2A
=tan2A ；
设tan2A=t，则t∈（0，1）；
上式化为t =
=
=﹣（t+1）﹣ +3≤﹣2 +3=3﹣2 ，
当且仅当t+1= ，即t= ﹣1时取“=”；
∴所求的最大值是3﹣2 ．
【考点精析】根据题目的已知条件，利用三角函数的最值的相关知识可以得到问题的答案，需要掌握函数，当时，取得最小值为；当时，取得最大值为，则，，．