题目内容
设同时满足条件:①
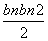 ≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界”数列.
≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界”数列.
(1)若数列{an}为等差数列,Sn是其前n项和:a3=4,S3=18,求Sn;
(2)判断(1)中的数列{Sn}是否为“特界”数列,并说明理由.
解:(1)设等差数列{an}的公差为d,
则a1+2d=4,S3=a1+a2+a3=3a1+3d=18,解得a1=8,d=-2,
∴Sn=na1+ d=-n2+9n.
d=-n2+9n.
(2){Sn}是“特界”数列,理由如下:
 故数列{Sn}适合条件①.
故数列{Sn}适合条件①.
而Sn=-n2+9n=- 2+
2+ (n∈N*),则当n=4或5时,Sn有最大值20,
(n∈N*),则当n=4或5时,Sn有最大值20,
即Sn≤20,故数列{Sn}适合条件②.
综上,数列{Sn}是“特界”数列.

练习册系列答案
相关题目
 米,树上另一点B离地面
米,树上另一点B离地面 米,某人在离地面
米,某人在离地面 米的C处看此树,则该人离此树________米时,看A,B的视角最大.
米的C处看此树,则该人离此树________米时,看A,B的视角最大.
 ,记数列{an}的前n项之积为Tr,则T2 013的值为( )
,记数列{an}的前n项之积为Tr,则T2 013的值为( ) B.-1
B.-1 ,矩形
,矩形 中,
中,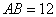 ,
,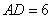 ,
,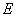 、
、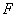 分别为
分别为 、
、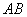 边上的点,且
边上的点,且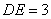 ,
,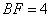 ,将
,将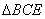 沿
沿 折起至
折起至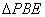 位置(如图
位置(如图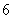 所示),连结
所示),连结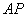 、
、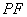 ,其中
,其中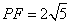 .
.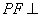 平面
平面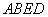 ;
; 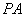 上是否存在点
上是否存在点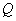 使得
使得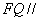 平面
平面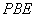 ?若存在,求出点
?若存在,求出点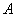 到平面
到平面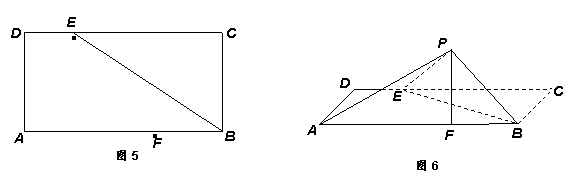

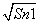 -Sn-1
-Sn-1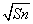 =2
=2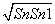 (n∈N*且n≥2),则a81=( )
(n∈N*且n≥2),则a81=( ) 有
有 个零点,则实数
个零点,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.